基于学习情况协同过滤算法的个性化学习推荐模型研究*

doi:10.11925/infotech.2096-3467.2019.1092

基于学习情况协同过滤算法的个性化学习推荐模型研究^*

苏庆, 陈思兆, 吴伟民, 李小妹^,^,, 黄佃宽

广东工业大学计算机学院广州 510006

Personalized Recommendation Model Based on Collaborative Filtering Algorithm of Learning Situation

Su Qing, Chen Sizhao, Wu Weimin, Li Xiaomei^,^,, Huang Tiankuan

School of Computers, Guangdong University of Technology, Guangzhou 510006, China

通讯作者: 李小妹,ORCID：0000-0002-8362-1018,E-mail:lixm@gdut.edu.cn。

收稿日期: 2019-09-30 修回日期: 2020-02-20 网络出版日期: 2020-05-25

基金资助:

*本文系国家留学基金委2018年国家—地方合作项目“高等教育教学法出国研修项目”. [2018]5028
2019年广东省高等教育教学改革项目“可视化WebIDE编程实训模式研究与应用”. SJJG20191216

2020年广东工业大学本科教学工程项目“面向编程实训教学的个性化推荐学习模式研究”的研究成果之一

Received: 2019-09-30 Revised: 2020-02-20 Online: 2020-05-25

摘要

【目的】 针对学习者学习过程中出现的信息过载问题,构建一个基于学习情况的个性化学习推荐模型LS-PLRM,为学习者推荐个性化学习方案。【方法】 在LS-PLRM中,提出一种应用三个学习情况因子改进相似度计算的PAD-CF协同过滤算法,结合知识地图与知识点度中心性实现知识点推荐度的计算与标注,最终生成个性化学习方案。【结果】 对于F值,LS-PLRM比Pearson-CF、Edurank、CF-SPM等学习推荐模型分别提高6.24%、2.68%和1.98%。对于得分提升率,LS-PLRM比上述模型分别提高3.85%、2.39%和1.41%。【局限】 未考虑多种复杂的学习情况影响因素,预测知识点得分的准确性有待提高。【结论】 个性化学习推荐模型LS-PLRM具有较高的实践应用意义。

关键词： 学习情况相似度 ; 协同过滤 ; 个性化学习 ; 推荐模型 ; 知识地图 ; 度中心性

Abstract

[Objective] This paper proposes a personalized model based on learning situation, which recommends schemes for learners and addresses the information overload issues.[Methods] First, we constructed a PAD-CF collaborative filtering algorithm based on three factors related to learning situation. Then, we introduced the knowledge map and degrees centrality of knowledge points to retrieve the recommended points.[Results] Compared to Pearson-CF, Edurank, and CF-SPM, the proposed model improved the F value by 6.24%, 2.68%, and 1.98%, respectively. The growth rates were 3.87%, 2.39%, and 1.43%.[Limitations] We need to add more complicated learning factors to improve the accuracy of predicted knowledge points.[Conclusions] The proposed model is highly practical for real world cases.

Keywords： Learning Situation Similarity ; Collaborative Filtering ; Personalized Learning ; Recommendation Model ; Knowledge Map ; Degree Centrality

PDF (1566KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

苏庆, 陈思兆, 吴伟民, 李小妹, 黄佃宽. 基于学习情况协同过滤算法的个性化学习推荐模型研究^*. 数据分析与知识发现[J], 2020, 4(5): 105-117 doi:10.11925/infotech.2096-3467.2019.1092

Su Qing, Chen Sizhao, Wu Weimin, Li Xiaomei, Huang Tiankuan. Personalized Recommendation Model Based on Collaborative Filtering Algorithm of Learning Situation. Data Analysis and Knowledge Discovery[J], 2020, 4(5): 105-117 doi:10.11925/infotech.2096-3467.2019.1092

1 引言

互联网的快速发展促进了学习资源和在线教育平台的大量涌现,然而海量的资源以及学习途径也导致信息过载（Information Overload）^[1]困境的出现。因此,研究高度自动化的个性化学习推荐模型,为学习者针对特定课程或领域推荐适合其自身学习情况的学习方案^[2],成为当前教育领域的研究热点之一。

个性化推荐算法（Personalized Recommendation Algorithm）^[3]是个性化学习推荐模型的核心支撑,包括基于协同过滤的推荐算法、基于内容的推荐算法和混合推荐算法等。其中基于用户的协同过滤（User-based Collaborative Filtering）算法^[4]以用户为中心,较为适用于个性化学习推荐领域。相似度计算是协同过滤算法的关键步骤。传统的相似度计算方法（如余弦相似度、修正的余弦相似度和皮尔逊相似度^[5]等）在应用于计算学习者之间的学习情况相似度时,会忽略与学习者有关的知识点掌握程度、知识点平均分以及测试题目难度差异等重要因素,影响计算准确度,使得对学习者的知识点预测得分出现偏差,进而影响最终的推荐效果。

因此,对协同过滤算法进行针对性改进,将其适配于个性化学习推荐领域,建立一种更适用于学习情况的个性化学习推荐模型（Personalized Learning Recommendation Model）^[6]具有重要的现实意义。

2 相关研究

近年来,基于网络学习的个性化学习推荐系统对于学习者的重要性逐渐显现^[2]。与一般的资源推荐算法不同,在面向学习资源的个性化推荐算法研究中,除了从学习者的兴趣点出发外,还需要考虑与学习者本身相关的个体特征因素。

2.1 学习推荐模型研究现状

在国内外学者对个性化学习推荐领域的研究中,有以下两方面值得关注：

（1）一些学者结合学习者学习情况等相关因素对传统的协同过滤算法做出改进,以期取得更好的学习推荐效果。Bobadilla等^[7]提出一种学习推荐算法New-cosine,该算法对每个学习者推荐的重要程度进行加权,提升学习成绩更好的学习者的推荐权重。Dwivedi等^[8]构建一个信任感知网络学习推荐系统TRCF-LS-KL,该系统结合学习者的学习风格、知识水平和不同学习者的信任度等方面对协同过滤算法进行改进。Bourkoukou等^[9]提出一种基于改进协同过滤算法和顺序模式挖掘的学习模型CF-SPM,该模型融合学习者的学习对象得分、学习时间和频率等以改进协同过滤算法,进而预测其他学习对象的得分,最后运用SPM算法对学习内容排序后进行推荐。Segal等^[10]提出联合协同过滤和社会选择理论的个性化学习推荐模型Edurank,通过协同过滤计算得到待推荐学生的相似学生集合,并根据相似学生集合在不同学习内容的答题情况,对学习内容进行难度排序,最后向学生推荐排序后的学习内容。

上述模型在实践中获得了不错的学习推荐效果,但仍然存在对学习者的学习情况相关因素挖掘不够充分和准确的共性问题,影响了学习情况相似度计算的准确性以及最终的推荐效果。因此,如何客观地挖掘和表征学习情况及其他相关因素,提高相似度计算结果的精确度,进而构建推荐效果更优的协同过滤模型,是值得进一步研究的方向。

（2）基于知识地图的学习推荐方法。这类学习资源推荐模式以知识地图为支撑,基于课程内容之间的内在联系进行学习资源推荐。Zheng等^[11]构建一个以知识地图为中心的学习系统Yotta,根据课程的知识结构特点及其逻辑关系创建知识地图,建立学习资源与知识单元的联系,根据学习者在不同知识单元中的学习情况推荐合适的学习资源。Wang等^[12]提出一个基于知识地图的知识共享社区模型,该模型通过结合学习系统特性,基于知识地图引导学习者在社区中共享知识内容。李士平等^[13]提出使用颜色标记知识点及其之间的关系类型、协同共建资源、自动生成学习路径等促进自我导向学习的策略,论证了知识地图在自我导向学习中起到的积极促进作用。柯立秋^[14]提出一种基于知识地图的学习资源融合系统,该系统从知识元关联关系出发,结合学习资源相关标准,建立知识元与学习资源间的关联。

上述基于知识地图的学习推荐模型存在一个明显缺陷：由于不具备对学习情况的预测功能,只能局限于在已有测试数据的学习范畴内进行知识点推荐,不能对其余知识点进行预测性推荐。该缺陷恰好可以通过协同过滤算法进行弥补,将知识地图融合运用于协同过滤学习推荐算法中,发展出一种具备高拓展性和准确度的学习推荐模型。

2.2 归纳与对比

基于研究现状,笔者归纳各种效果较为明显的基于改进协同过滤算法的主流推荐算法模型如表1所示。

表1 经典推荐模型归纳

Table 1 Introduction of Classical Recommendation Model

算法模型	优势	不足
Pearson-CF^[15]	是经典的协同过滤算法,结合学习者的共同知识点平均分,使得相似度的计算更具客观性。	由于忽略了体现学习者学习情况的各种因素,导致相似度计算结果准确度欠佳。
New-cosine^[7]	引入权重方程,提升了学习成绩较好学习者的推荐权重,进而改进协同过滤算法。	学习者的学习情况各异,仅以成绩较好的学习者作为推荐标准,缺乏个性化,影响推荐效果。
TRCF-LS-KL^[8]	结合学习者学习风格、知识水平及信任模式对协同过滤算法进行改进。	仅通过问卷调查手段确定学习风格相对片面;由学习者指定被信任人的信任模式具有较大主观性。
CF-SPM^[9]	融合学习者的学习情况（学习对象得分）以及学习风格（学习某对象的时间、频率）改进协同过滤算法。	仅以学习时间和频率等个体差异较大的因素计算学习者的相似度时,存在较大偏差,客观性不足。
Edurank^[10]	联合协同过滤和社会选择理论,结合学习者以及相似学习群体的学习情况和认知水平改进协同过滤算法。	缺乏对学习者自身学习情况和学习风格等方面信息的挖掘,与个性化学习情况的结合程度较低。

新窗口打开| 下载CSV

由上述研究成果可知,忽略学习者在学习过程中展现的各种学习情况属性以及知识点之间的内在联系会明显地影响学习推荐模型的效果。因此,本文提出一种融合知识地图、度中心性以及协同过滤算法的个性化学习推荐模型（Learning Situation Based Personalized Learning Recommendation Model, LS-PLRM）。在LS-PLRM中,一方面引入知识点掌握程度相似性因子、平均分相似性因子和知识点难度系数修正因子,设计一种基于学习情况的相似度计算方法,在此基础上构造一种基于学习情况的协同过滤算法;另一方面通过挖掘课程知识点之间的内在联系,构建课程知识地图。

与上述其他模型相比,本文提出的LS-PLRM注重合理体现学习者学习情况的关键因素,更准确地获得学习情况相似度的计算结果,进而实现对协同过滤算法的改进;同时通过构建引入知识点度中心性的课程知识地图,并基于此进行知识点的个性化推荐,可以帮助学习者更好地掌握知识脉络,减少学习者在学习过程中的认知负担,提升学习效率。

3 知识地图及知识点的度中心性

由知识模块及知识点构建而成的知识地图可以令学习者在学习过程中更加清晰地了解某一课程或者领域的知识体系结构,而知识点的度中心性可作为在知识地图中优先推荐的相对重要知识点的依据。

3.1 课程知识地图模型

知识地图（Knowledge Map）^[16]是一个有向无环图,是一种知识编码方法^[17],展示和解释了“关于知识的知识”^[18]。本文将知识地图应用于具体课程,分析课程领域内章、节、知识点间的内在逻辑关系,构建网络化的知识结构图。

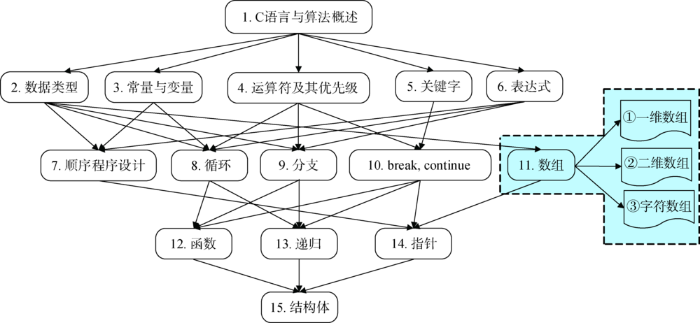
以《C语言程序设计》课程为例,构造其课程知识地图如图1所示。该课程知识地图包含两大类节点：知识模块和知识点,其中知识模块是一个或多个密切相关的知识点集合。图1中序号1-15的节点为知识模块。另外,以知识模块“11.数组”为例,列举了隶属于该模块的①-③知识点（见虚线框部分）。其他知识模块也包含数量不等的知识点,由于篇幅所限而不再详细列出。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 《C语言程序设计》课程知识地图

Fig.1 Knowledge Map of C Programming

3.2 知识点的度中心性

度中心性（Degree Centrality）用于描述节点在网络结构中的重要程度。一个节点的邻居数目越多,其重要程度就越高^[19]。应用于学习推荐领域,度中心性可以衡量一个知识点在课程知识地图的重要程度：度中心性大的知识点一般处于课程知识地图的中心;而度中心性小的知识点一般处于课程知识地图的边缘位置。在知识地图中,知识点隶属于知识模块,为简化计算,可将隶属于同一知识模块的所有知识点的重要程度看作是相同的,因此它们的度中心性也相同。基于同样假设,可将知识点的度中心性等同于所在知识模块的度中心性。某知识模块 $m_{i}$ 的度中心性 $C_{D} (m_{i})$ 如公式（1）所示。

(1)

C_{D} (m_{i}) = \frac{\sum_{j} z_{ij}}{h - 1}, i \neq j

其中, $z_{ij}$ 为 $m_{i}$ 与 $m_{j}$ 之间存在直接关联的次数;h为知识模块数量的总和。

4 基于学习情况的协同过滤算法

本文提出一种适配于个性化学习推荐的协同过滤算法（Collaborative Filtering with Learning Proficiency, Average Score and Topic Differences, PAD-CF）,引入知识点掌握程度相似性因子、平均分相似性因子和知识点难度系数修正因子,设计一种基于学习情况的相似度计算方法;运用K近邻算法,筛选出相似度最高的TOP-N个学生作为邻居集合;通过该邻居集合计算学生的知识点预测得分,以此作为推荐结果的重要依据之一。

4.1 基于学习情况的相似度计算方法

本文提出一种基于学习情况的相似度计算方法,对传统的Pearson相似度公式进行改进,使其适配于个性化学习推荐领域。不同学生相似度的计算,实质上是计算不同学生在某门课程上学习情况相关因素的相似性。

为体现不同学生在某门课程的掌握程度,引入知识点掌握程度相似性因子（Proficiency Factor,p）,不同学生对知识点的掌握程度相似性越高,表明学生在学习情况上越接近。为描述不同学生对某门课程的总体掌握程度,引入平均分相似性因子（Average Score Factor,a）,不同学生在知识点平均分上相似性越高,表明学生在学习情况上越接近。另外,用于考查同一个知识点的不同题目不可避免地存在难度上的差异,当抽取这些题目进行组卷时,会导致同一个知识点在不同试卷中所表现出的难度系数存在差别,因此引入知识点难度系数修正因子（Difference Factor,d）。

本文提出的三个因子相互关联,并且构成了对学生学习情况的整体表征。p和a是从学生对课程的学习情况出发,总体把握学生之间对课程掌握程度的相似性,用于挖掘学生学习课程的学习情况特性。另外,不同试题产生的知识点难度系数差异会影响计算p和a的准确度,最终影响学生之间相似度计算的准确性,因此需引入知识点难度系数修正因子d,以限制知识点难度系数差异带来的影响。

基于上述三个因子形成一种基于学习情况的相似度计算方法,从学习者的学习情况和认知水平出发,同时考虑课程特性并通过修正因子降低知识点难度系数差异。该方法能较为充分和准确地计算学习情况的相似度,进而提升知识点得分预测的准确性。

假设考查学生 $s_{i}$ 和 $s_{j}$ 的试卷不相同,因而属于不同的学生集合 $S_{1}$ 和 $S_{2}$ , $Si m_{pad} (s_{i}, s_{j})$ 表示 $s_{i}$ 和 $s_{j}$ 学习情况的相似度,计算方法如公式（2）所示。

(2)

Si m_{pad} (s_{i}, s_{j}) = p_{s_{i}, s_{j}} \times a_{s_{i}, s_{j}} \times \frac{\sum_{x \in X} ({r^{'}}_{s_{i}, x} - \bar{{r^{'}}_{s_{i}}}) (r_{s_{j}, x} - \bar{r_{s_{j}}})}{\sqrt[]{{\sum_{x \in X} ({r^{'}}_{s_{i}, x} - \bar{{r^{'}}_{s_{i}}})}^{2}} \sqrt[]{{\sum_{x \in X} (r_{s_{j}, x} - \bar{r_{s_{j}}})}^{2}}} x \in X = Z_{1} ⋂ Z_{2}

其中, $r'_{s_{i}, x}$ 和 $\overset{'_{s_{i}}}{r}$ 的计算方法如公式（3）和公式（4）所示。

(3)

r'_{s_{i}, x} = d_{S_{1}, S_{2}} \times r_{s_{i}, x}

(4)

\overset{'_{s_{i}}}{r} = d_{S_{1}, S_{2}} \times \bar{r_{s_{i}}}

其中, $p_{s_{i}, s_{j}}$ 为知识点掌握程度相似性因子, $a_{s_{i}, s_{j}}$ 为平均分相似性因子, $d_{S_{1}, S_{2}}$ 为知识点难度系数修正因子, $Z_{1}$ 和 $Z_{2}$ 分别是用于考查 $s_{i}$ 和 $s_{j}$ 的题目所关联的知识点集, $X$ 是用于考查 $s_{i}$ 和 $s_{j}$ 的题目所关联的公共知识点集, $r_{s_{i}, x}$ 和 $\bar{r_{s_{i}}}$ 分别是 $s_{i}$ 在知识点x上的得分和在 $X$ 上的平均分（本文中的知识点得分都已归一化）, $r'_{s_{i}, x}$ 和 $\overset{'_{s_{i}}}{r}$ 分别是 $s_{i}$ 引入 $d_{S_{1}, S_{2}}$ 后在x上的得分和在 $X$ 上的平均分, $r_{s_{j}, x}$ 和 $\bar{r_{s_{j}}}$ 分别是 $s_{j}$ 在x上的得分和在 $X$ 上的平均分。

（1）知识点掌握程度相似性因子

在学习某门课程时,不同学生对于各个知识点会有不同的掌握程度。知识点掌握程度相似性因子p用于描述学生 $s_{i}$ 和 $s_{j}$ 对于同一门课程知识点掌握程度的相似性,计算方法如公式（5）所示。

(5)

p_{s_{i}, s_{j}} = \frac{| X_{s_{i}, s_{j}}^{p} | + | X_{s_{i}, s_{j}}^{np} |}{| Z_{1} ⋂ Z_{2} |}

其中, $| X_{s_{i}, s_{j}}^{p} |$ 是 $s_{i}$ 和 $s_{j}$ 共同掌握的知识点数量, $| X_{s_{i}, s_{j}}^{np} |$ 是 $s_{i}$ 和 $s_{j}$ 都未掌握的知识点数量, $| Z_{1} ⋂ Z_{2} |$ 是用于考查 $s_{i}$ 和 $s_{j}$ 的题目所关联的公共知识点的数量。

$p_{s_{i}, s_{j}}$ 值越大,表示 $s_{i}$ 和 $s_{j}$ 在该课程学习中知识点的掌握程度越相似。另外,判定一个知识点是否达到掌握程度的阈值取值区间为[0,1],可以根据课程具体需要而确定,一般情况下可取0.6。

（2）平均分相似性因子

从考试成绩的角度,学生对于某门课程的学习情况还可以由知识点的平均分来表征,如果两个学生在某门课程的知识点平均分越接近,则他们学习情况的相似程度就越高,由此引入平均分相似性因子a。某两位学生 $s_{i}$ 和 $s_{j}$ 的平均分相似性因子 $a_{s_{i}, s_{j}}$ 的计算方法如公式（6）所示。

(6)

a_{s_{i}, s_{j}} = r_{f} - |\bar{r_{s_{i}, all}} - \bar{r_{s_{j}, all}}|

其中, $r_{f}$ 是知识点的满分分值,其值为1.0, $\bar{r_{s_{i}, all}}$ 、 $\bar{r_{s_{j}, all}}$ 分别是 $s_{i}$ 和 $s_{j}$ 在所有知识点得分的平均分。

$|\bar{r_{s_{i}, all}} - \bar{r_{s_{j}, all}}|$ 越小,表示 $s_{i}$ 和 $s_{j}$ 在这门课程的学习情况越接近,此时 $a_{s_{i}, s_{j}}$ 的值越大;反之同理。

（3）知识点难度系数修正因子

用于考查同一个知识点的不同题目存在难度上的差异。当抽取这些题目进行组卷时,会导致某知识点在不同试卷中所表现出的难度系数有差异。引入知识点难度系数修正因子d可以减小该差异,学生 $s_{i}$ 和 $s_{j}$ 分别属于学生集合 $S_{1}$ 和 $S_{2}$ （用于考查 $S_{1}$ 和 $S_{2}$ 的试卷不同）,计算方法如公式（7）所示。

(7)

d_{S_{1}, S_{2}} = \frac{\bar{r_{S_{1}, x}}}{\bar{r_{S_{2}, x}}} x \in X = Z_{1} ⋂ Z_{2}

其中, $X$ 是用于考查 $S_{1}$ 和 $S_{2}$ 的题目所关联的公共知识点集, $\bar{r_{S_{1}, x}}$ 、 $\bar{r_{S_{2}, x}}$ 分别是 $S_{1}$ 和 $S_{2}$ 在同一知识点x的平均得分。

4.2 基于K近邻算法的知识点得分预测

K近邻（K-Nearest Neighbor）算法的基本思想^[20]是：如果一个样本在特征空间中的K个最相似（即特征空间中最邻近）样本中的大多数属于某一个类别,则推断该样本也属于这个类别。

对于某一学生 $s_{i} \in S_{1}$ ,利用公式(2)计算 $s_{i}$ 与 $S_{2}$ 中所有学生的相似度,然后利用K近邻算法筛选出与 $s_{i}$ 相似度最高的TOP-N个学生,构成邻居集合 $W$ , $W \subseteq S_{2}$ 。根据 $W$ ,可以预测 $s_{i}$ 在未测知识点y上的分数 $Fs (s_{i}, y)$ ,如公式（8）所示。

(8)

Fs (s_{i}, y) = \bar{r_{s_{i}}} + \frac{\sum_{s_{j} \in W} Si m_{pad} (s_{i}, s_{j}) (r_{s_{j}, y} - \bar{r_{s_{j}}})}{\sum_{s_{j} \in W} Si m_{pad} (s_{i}, s_{j})}

y \in Y = Z_{1} - Z_{1} ⋂ Z_{2}

其中, $Si m_{pad} (s_{i}, s_{j})$ 为应用公式(2)计算得到的 $s_{i}$ 与 $s_{j} \in W$ 的相似度, $Y$ 是未用于考查 $s_{i}$ 的知识点集, $r_{s_{j}, y}$ 是 $s_{j}$ 在知识点 $y$ 上的得分。

5 融合知识地图、度中心性与协同过滤的个性化学习推荐模型

5.1 个性化学习推荐模型的构建

在个性化学习推荐模型LS-PLRM中,基于知识点的度中心性,运用协同过滤算法PAD-CF计算知识点推荐度,将其标注于知识地图的知识点中,最终形成学习者的个性化学习方案。

个性化学习方案以课程知识地图作为载体。知识地图中的知识点对应唯一的推荐度。推荐度越高的知识点,越应当引起学习者的重视。推荐度由知识点的度中心性与学习者在知识点的失分分值计算得到,其中度中心性高的知识点表示该知识点在知识网络中的重要程度高;而失分分值高的知识点表明学习者对该知识点的掌握程度较低。

对于某学生 $s_{i}$ ,由已测知识点x所属知识模块 $m_{j}$ 的度中心性 $C_{D} (m_{j})$ 及其失分分值 $[r_{f} - r_{s_{i}, x}]$ ,可计算x的推荐度,如公式（9）所示。

(9)

\begin{array}{l} Rec (s_{i}, x, m_{j}) = w_{1} C_{D} (m_{j}) + w_{2} [r_{f} - r_{s_{i}, x}] \\ x \in X = Z_{1} ⋂ Z_{2} \end{array}

同理,对于未测知识点y,其所属知识模块 $m_{k}$ 的度中心性为 $C_{D} (m_{k})$ ,预测失分分值为 $[r_{f} - Fs (s_{i}, y)]$ ,推荐度计算如公式（10）所示。

(10)

\begin{array}{l} Rec (s_{i}, y, m_{k}) = w_{1} C_{D} (m_{k}) + w_{2} [r_{f} - Fs (s_{i}, y)] \\ y \in Y = Z_{1} - Z_{1} ⋂ Z_{2} \end{array}

其中, $w_{1}$ 是知识点x或y所属知识模块度中心性的权重因子; $w_{2}$ 是知识点失分分值权重因子。

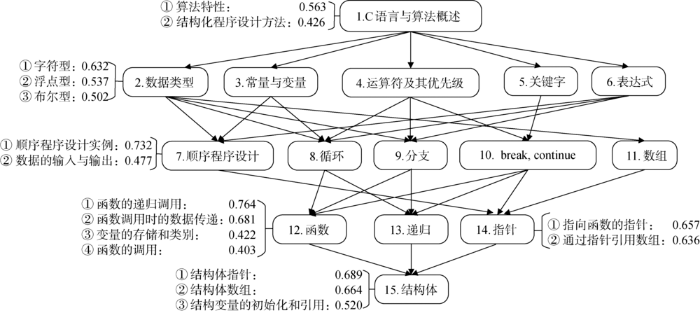
将推荐度标注于知识地图的知识点中,可形成学习者的个性化学习方案。方案所推荐的知识点均为学习者尚未掌握的知识点。以某同学为例,LS-PLRM为其生成的《C语言程序设计》课程的个性化学习方案（局部）如图2所示（由于篇幅所限,仅列举出6个知识模块的知识点推荐度）。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 个性化学习方案示例

Fig.2 Example of Personalized Learning Scheme

5.2 个性化学习推荐模型实施流程

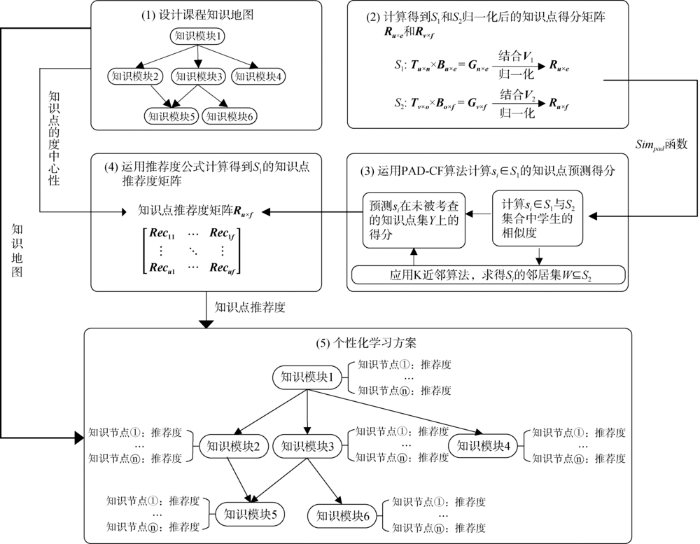
基于课程知识地图、度中心性以及基于学习情况的协同过滤算法,构造LS-PLRM推荐模型的实施框架,其实施流程如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 LS-PLRM的实施框架

Fig.3 Framework of LS-PLRM

（1）建立课程知识地图,并计算所有知识模块的度中心性,进而得到所有知识点的度中心性。

（2）设有学生集合 $S_{1}$ 和 $S_{2}$ ,包含学生数分别为u和v;用于考查 $S_{1}$ 和 $S_{2}$ 的题目集分别为 $Q_{1}$ 和 $Q_{2}$ ,题目数分别为n和o; $Q_{1}$ 和 $Q_{2}$ 所关联的知识点集分别为 $Z_{1}$ 和 $Z_{2}$ ,知识点数分别为e和f, $Z_{1}$ 和 $Z_{2}$ 中的知识点满分分值向量分别为 $V_{1} = {α_{1}, α_{2}, \dots, α_{e}}$ 和 $V_{2} = {β_{1}, β_{2}, \dots, β_{f}}$ ;引入题目-知识点关联矩阵 $B_{n \times e}$ 和 $B_{o \times f}$ （每一行代表某一道题目中出现的知识点,每一列代表某一个知识点出现在哪些题目中）; $S_{1}$ 和 $S_{2}$ 的题目得分矩阵分别为 $T_{u \times n}$ 和 $T_{v \times o}$ （每一行代表某一个学生在每个题目的得分,每一列代表不同学生在某一道题目的得分）,对应的知识点得分矩阵分别为 $G_{u \times e}$ 和 $G_{v \times f}$ （每一行代表某一个学生在每个知识点的得分,每一列代表每个学生在某一个知识点的得分）,进行归一化后的知识点得分矩阵分别为 $R_{u \times e}$ 和 $R_{v \times f}$ 。

①据学生的试卷得分情况,分别获取 $S_{1}$ 和 $S_{2}$ 的 $T_{u \times n}$ 和 $T_{v \times o}$ ;

②结合 $B_{n \times e}$ 和 $B_{o \times f}$ ,计算 $G_{u \times e} = T_{u \times n} \times B_{n \times e}$ 和 $G_{v \times f} = T_{v \times o} \times B_{o \times f}$ ;

③对 $G_{u \times e}$ 和 $G_{v \times f}$ 进行归一化处理。对于 $g_{ij} \in G_{u \times e}$ ,有 $r_{ij} = g_{ij} / α_{j}$ ,其中 $r_{ij} \in R_{u \times e}$ , $α_{j} \in V_{1}$ 。该过程是将知识点得分 $g_{ij}$ 映射到区间[0,1],得到归一化后的知识点得分矩阵 $R_{u \times e}$ ;同理使用 $G_{v \times f}$ 和 $V_{2}$ 可计算得到 $R_{v \times f}$ 。

（3）运用PAD-CF算法计算某一学生 $s_{i} \in S_{1}$ 在知识点 $y$ 上的预测分数 $Fs (s_{i}, y)$ 。

（4）对于 $s_{i}$ ,运用公式(9)和公式(10)计算所有课程知识点的推荐度。

（5）将各个知识点的推荐度标注于课程知识地图中,得到一个以课程知识地图形式呈现的个性化学习方案。学习者可以结合自身学习该课程的需求,按照知识模块层级、知识模块顺序以及各个知识点推荐度的高低对该门课程进行针对性学习。

6 实验及结果分析

（1）实验一：将个性化学习推荐模型LS-PLRM与其他推荐模型进行有效性方面的对比验证;

（2）实验二：基于实验一将个性化学习推荐模型应用于实际的学习者群体,运用分组对比策略,与其他推荐模型作实际应用效果的对比验证。

6.1 实验数据采集

为验证个性化学习推荐模型的有效性,采集三组数据集：dataset_one、dataset_two和dataset_three,均来自广东某高校学生的期末考试数据以及两次测验的实际数据。

（1） dataset_one

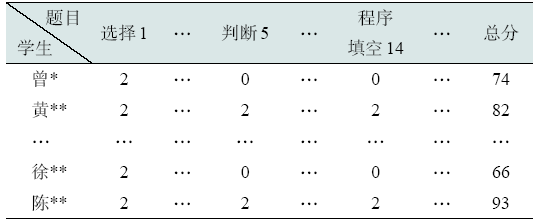
采集自往届学生《C语言程序设计》期末考试成绩,共包含1 430位学生的考试得分,所用试卷共有题目50道,涉及知识点59个。dataset_one用于验证PAD-CF协同过滤算法的有效性,为应用于其中学生学习情况相似度的计算,需要按各道题目得分分别处理。采集到学生的题目得分矩阵,如表2所示。

表2 学生的题目得分矩阵

Table 2 Scoring Matrix of Students

新窗口打开| 下载CSV

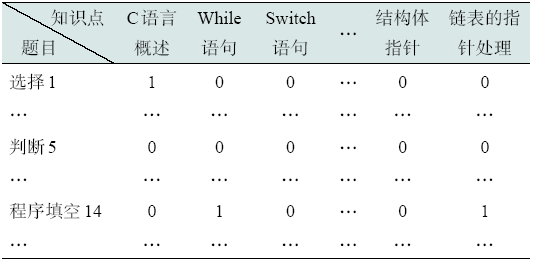
通过分析试卷中题目所考查的知识点,得到题目-知识点关联矩阵如表3所示（其中1代表该题目考查了该知识点,0代表未考查）。

表3 题目-知识点关联矩阵

Table 3 Incidence Matrix of Question and Knowledge Point

新窗口打开| 下载CSV

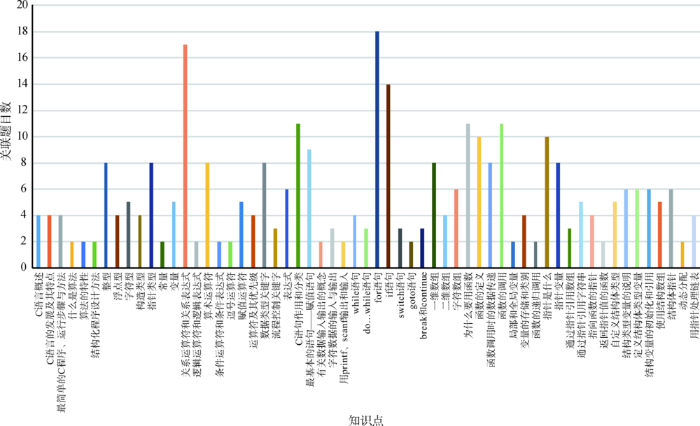
作为期末考试,试卷中涵盖了绝大部分知识点,各知识点所关联的题目数量如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 dataset_one中各知识点所关联的题目数量

Fig.4 Question Quantity Associated with Knowledge Points in dataset_one

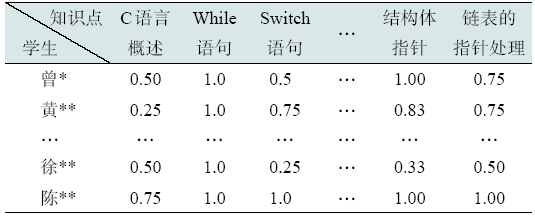
结合题目得分矩阵和题目-知识点关联矩阵,计算得到学生在各个知识点上的得分矩阵,然后对知识点得分进行归一化处理,得到归一化后的知识点得分矩阵如表4所示,由此构成dataset_one。

表4 归一化后的知识点得分矩阵

Table 4 Normalized Scoring Matrix of Knowledge Point

新窗口打开| 下载CSV

（2） dataset_two和dataset_three

dataset_two和dataset_three采集自参与本实验学生的两次对比测试的题目得分,用于验证个性化学习推荐模型的实用性。

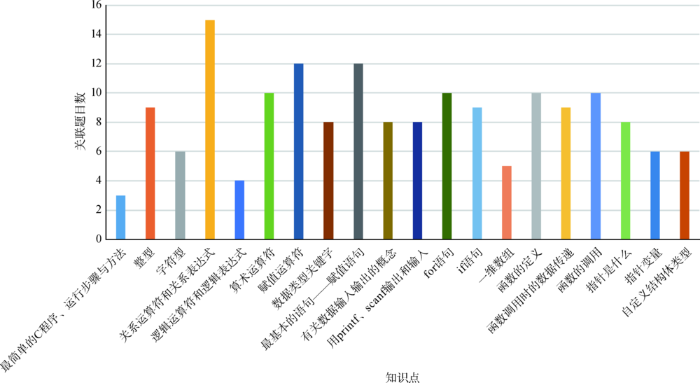
其中dataset_two采集自这些学生第一次测试的题目得分。dataset_two中共包含153位学生的测验得分,所用试卷共有44道题目,涉及20个知识点。同样需要按各道题目得分分别处理（过程参考dataset_one）,获得归一化后的知识点得分矩阵,由此构成dataset_two。各知识点所关联的题目数量如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 dataset_two中各知识点所关联的题目数量

Fig.5 Question Quantity Associated with Knowledge Point in dataset_two

dataset_three采集自上述学生第二次测试的题目得分。

6.2 实验评价指标

分别通过准确率（precision）、召回率（recall）和F值评价推荐知识点的准确性,通过平均绝对误差（MAE）^[21]衡量知识点预测得分与实际得分的接近程度。各指标的计算方法如公式（11）-公式（14）所示。

(11)

precision = \frac{CorrectRec}{TotalRec}

(12)

recall = \frac{CorrectRec}{TotalNotPro}

(13)

F = \frac{2 \times precision \times recall}{precision + recall}

(14)

MAE = \frac{\sum_{l=1}^{N} | l_{i} - \overset{̑}{l_{i}} |}{N}

其中, $CorrectRec$ 是正确推荐的知识点（即学生需要掌握但未掌握的知识点）, $TotalRec$ 是推荐知识点的总数, $TotalNotPro$ 是学生未掌握的知识点总数, $l_{i}$ 是对知识点 $i$ 的预测值, $\overset{̑}{l_{i}}$ 是dataset_one中学生知识点 $i$ 的真实得分。

另外,通过得分提升率（GrowthRate）衡量各组学生使用不同推荐模型的效果,如公式（15）所示。

(15)

Growt h Rate = \frac{ImprovedScore}{FirstTextScore}

其中,ImprovedScore是增长的分数,FirstTextScore是第一次测试的分数。

6.3 实验对比及分析

在实验中,将LS-PLRM与Pearson-CF、CF-SPM和Edurank等模型进行对比。选择这些模型进行对比的原因是：Pearson-CF是经典的协同过滤算法,其应用面较广;CF-SPM和Edurank是近年新提出的学习推荐模型,在方法上具有较高的创新性,并且已在实验中取得了较好的推荐效果。

（1）实验一：验证个性化学习推荐模型的理论有效性

本实验使用dataset_one数据集,该数据集采集自学生期末考试的题目得分,题目具有较强的代表性,适合作为验证不同协同过滤算法有效性的数据集。从dataset_one中抽取90%作为训练集（包含1 287位学生数据）;另外10%作为验证集（包含143位学生数据）。

对于《C语言程序设计》,实验表明 $w_{1}$ 取0.3, $w_{2}$ 取0.7时的推荐效果最佳,因此在后续实验中, $w_{1}$ 和 $w_{2}$ 都是取上述值。

各推荐模型在指标值precision、recall和F值上的实验结果如表5所示。可以看出,LS-PLRM的实验结果优于其余三种推荐模型,表明LS-PLRM模型能够更加准确地为学生推荐知识点。

表5 应用不同推荐模型的指标值

Table 5 Indicator Values of Recommendation Models

TOP-N	推荐模型	precision	recall	F
5	Pearson-CF	0.609 4	0.551 4	0.579 0
	Edurank	0.630 6	0.578 5	0.603 4
	CF-SPM	0.653 9	0.599 7	0.625 6
	LS-PLRM	0.679 4	0.616 4	0.646 4
10	Pearson-CF	0.623 5	0.564 7	0.592 6
	Edurank	0.657 5	0.583 5	0.618 3
	CF-SPM	0.696 5	0.606 5	0.648 4
	LS-PLRM	0.730 5	0.614 9	0.667 7
15	Pearson-CF	0.644 6	0.574 1	0.607 3
	Edurank	0.682 1	0.593 1	0.634 5
	CF-SPM	0.717 0	0.605 0	0.656 3
	LS-PLRM	0.728 7	0.621 6	0.670 9
20	Pearson-CF	0.654 7	0.585 2	0.618 0
	Edurank	0.716 6	0.600 8	0.653 6
	CF-SPM	0.717 8	0.611 9	0.660 6
	LS-PLRM	0.737 9	0.631 2	0.680 4

新窗口打开| 下载CSV

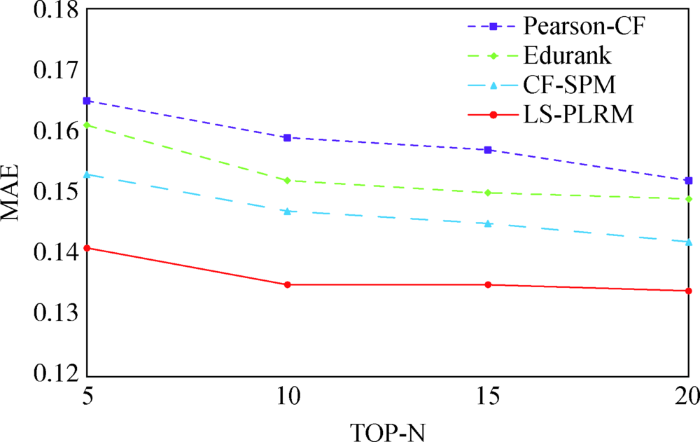
MAE反映知识点预测得分的准确性,MAE值越低,说明该协同过滤算法能够更加准确地预测知识点得分。由于知识点得分进行了归一化处理,各算法模型的MAE值较低,如图6所示,可以发现LS-PLRM模型比Pearson-CF、Edurank、CF-SPM在MAE值上分别降低11.84%、10.07%、5.63%,知识点预测得分与实际得分的接近程度更高,因此预测的知识点得分更为准确。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 各种推荐模型的MAE指标值对比

Fig.6 MAE Values of Recommendation Models

（2）实验二：验证个性化学习推荐模型的实际有效性

参与本实验的学生共有153名,大致均分为4个小组验证个性化学习推荐模型的有效性。本实验分为两次测试,在第一次测试之后,学生根据不同推荐模型学习两周,然后进行第二次测试。各组的人数及采用的推荐模型如表6所示。

表6 分组信息及采用的推荐模型

Table 6 Grouping Information and Recommendation Models

组别	人数	推荐模型
A	38	Pearson-CF
B	39	Edurank
C	38	CF-SPM
D	38	LS-PLRM

新窗口打开| 下载CSV

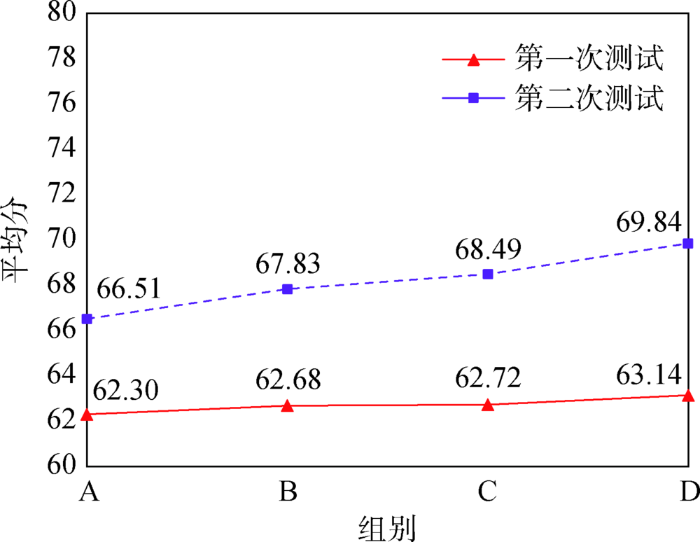
各组学生在两次测试中的平均分如图7所示,可以看出,A、B、C和D组在第二次测试中的平均分比第一次分别提升4.21、5.15、5.77和6.70,得分提升率分别为6.76%、8.22%、9.20%和10.61%。因此,LS-PLRM模型相比其他推荐模型的有更好的应用效果。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 两次测试中的平均分对比

Fig.7 Average Scores in Two Tests

为进一步分析4组学生经过不同推荐模型学习之后的差异性,采用数据分析工具SPSS对第二次测试作特别适用于小样本规模的T检验分析^[22]。由于实验需要,各组人数需保持一致,因此在B组随机减少一名学生。分组样本统计如表7所示,分组成对样本检验如表8所示。可知各组应用不同模型进行学习之后,D组较其他组的测试得分均值更高,表明LS-PLRM的推荐效果更佳;标准差和均值的标准误差更低,表明经过LS-PLRM学习的学生群体成绩更加均衡,分离度较小。

表7 分组样本统计

Table 7 Statistics of Sub-samples

Group	N	Mean	Std.Deviation	Std.Error.Mean
A	38	66.51	11.31	1.83
B	38	67.56	11.06	1.79
C	38	68.49	8.96	1.45
D	38	69.84	8.48	1.38

新窗口打开| 下载CSV

表8 分组成对样本检验

Table 8 Test of Paired Sub-samples

Group	t	sig(2-tailed)
comparison: A-D	-2.59	0.014
comparison: B-D	-2.39	0.022
comparison: C-D	-2.14	0.039

新窗口打开| 下载CSV

结合表8的t值和sig.(2-tailed)值可以进一步发现,D组与A、B、C相比,sig.(2-tailed)值均小于0.05,表明D组学生的分数与其他各组有显著性差异,使用LS-PLRM进行学习的D组学生取得更好的提升效果,也体现了LS-PLRM在个性化学习推荐领域的有效性。

7 结语

本文构建一种基于学习情况协同过滤算法的个性化学习推荐模型LS-PLRM。在LS-PLRM中,提出一种应用三个学习情况因子以改进相似度计算的PAD-CF协同过滤算法,同时结合知识地图与知识点度中心性进行知识点推荐度的计算与标注,最终生成个性化学习方案。实验结果表明,相比于其他推荐模型,LS-PLRM的推荐知识点准确性更高,证明了LS-PLRM的有效性;同时在实际应用中,学生根据LS-PLRM生成的个性化学习方案学习之后,整体的学习效果有明显提升。

在LS-PLRM模型中,对学习情况影响因素的挖掘尚不够充分;另外,在知识地图的构建过程中,对知识点内在关联的考虑也未够细致。在未来研究中,将考虑更加丰富的学习情况影响因素,进一步提升预测知识点得分的准确性;并构建更为完善的知识地图,以达到更好的推荐效果。

作者贡献声明

苏庆：提出研究思路,设计研究方案,论文修订;

陈思兆：设计研究方案,技术实现,进行实验,论文起草;

吴伟民：研究方案修正,论文修订;

李小妹：论文最终版本修订;

黄佃宽：实验数据分析与整理。

利益冲突声明

所有作者声明不存在利益冲突关系。

支撑数据

支撑数据由作者自存储,E-mail: sizhao_chen@163.com。

[1] 陈思兆,李小妹. dataset_one.xlsx. 1430位学生期末成绩及归一化后知识点得分.

[2] 陈思兆,李小妹. dataset_two.xlsx. 153位学生第一次测试的成绩.

[3] 陈思兆,李小妹. dataset_three.xlsx. 153位学生第二次测试的成绩.

[4] 陈思兆,李小妹. knowledgePointsNumber.xlsx. 题目关联知识点数量.

[5] 陈思兆,李小妹. incidenceMatrix.xlsx. 题目-知识点关联矩阵表.

[6] 陈思兆,李小妹. examination.rar. 第一次&第二次测试试卷及答案.

[7] 陈思兆,李小妹. recommend.xlsx. 模型生成153位学生的推荐结果（包括推荐知识点及对应推荐度）.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Tarus J

, Niu

, Mustafa

Knowledge-based Recommendation: A Review of Ontology-based Recommender Systems for E-learning

[J]. Artificial Intelligence Review, 2018,50:21-48.

算法模型	优势	不足
Pearson-CF^[15]	是经典的协同过滤算法,结合学习者的共同知识点平均分,使得相似度的计算更具客观性.	由于忽略了体现学习者学习情况的各种因素,导致相似度计算结果准确度欠佳.
New-cosine^[7]	引入权重方程,提升了学习成绩较好学习者的推荐权重,进而改进协同过滤算法.	学习者的学习情况各异,仅以成绩较好的学习者作为推荐标准,缺乏个性化,影响推荐效果.
TRCF-LS-KL^[8]	结合学习者学习风格、知识水平及信任模式对协同过滤算法进行改进.	仅通过问卷调查手段确定学习风格相对片面;由学习者指定被信任人的信任模式具有较大主观性.
CF-SPM^[9]	融合学习者的学习情况（学习对象得分）以及学习风格（学习某对象的时间、频率）改进协同过滤算法.	仅以学习时间和频率等个体差异较大的因素计算学习者的相似度时,存在较大偏差,客观性不足.
Edurank^[10]	联合协同过滤和社会选择理论,结合学习者以及相似学习群体的学习情况和认知水平改进协同过滤算法.	缺乏对学习者自身学习情况和学习风格等方面信息的挖掘,与个性化学习情况的结合程度较低.