基于本体的语义相似度计算方法研究综述
[孙海霞1 
, 钱庆1 , 成颖2 ]
, 钱庆引用本文
孙海霞, 钱庆, 成颖. 基于本体的语义相似度计算方法研究综述. 现代图书情报技术, 2010, 26(1): 51-56
Sun Haixia, Qian Qing, Cheng Ying. Review of Ontology-based Semantic Similarity Measuring. New Technology of Library and Information Service, 2010, 26(1): 51-56
Permissions
Sun Haixia, Qian Qing, Cheng Ying. Review of Ontology-based Semantic Similarity Measuring. New Technology of Library and Information Service, 2010, 26(1): 51-56
Copyright©2010, The modern information technology editorial office
This article is the open access journal literature, in the following situations are free to use: academic research and academic exchanges, scientific research and teaching, etc., but don't allow for commercial purposes.
基于本体的语义相似度计算方法研究综述
摘要
在对基于本体的词语语义相似度进行界定的基础上,对基于本体的语义相似度研究进行综述,分别阐述基于距离的语义相似度计算、基于内容的语义相似度计算、基于属性的语义相似度计算和混合式语义相似度计算等算法模型,最后从宏观层面指出今后本领域的研究方向。
结果(篇数)
关键词:
语义相似度; 语义相似度计算; 本体; 概念匹配
Review of Ontology-based Semantic Similarity Measuring
Abstract
Based on the general definition and dissertation for semantic similarity measuring of Ontology, this paper makes a review of research on the Ontology-based semantic similarity measures,introduces edge counting measures, information content measures, feature-based measures and hybrid measures respectively. At last, it points out the direction of future work from macroscopic perspective.
Keyword:
Semantic similarity; Semantic similarity measuring; Ontology; Concept-based matching
1 引 言
与前些年的信息资源匮乏相比,现在信息用户更加关注的是如何从海量的信息资源中发掘其所需要的信息。信息资源异构性的存在,尤其是语义异构性的存在,使得采用传统以字符串匹配为基础的信息检索系统难以满足用户对信息和知识的深层次需求,因此,加强基于概念匹配的信息检索系统的研究就显得尤为重要。简而言之,概念匹配就是计算词语之间的语义相似度[ 1]。与传统的以词形为切入点、建立在词语字面匹配基础上的检索算法相比,语义相似度计算是对源和目标词语间在概念层面上相似程度的度量,需要考虑词语所在的语境和语义等信息。本体[ 2]因其能够准确描述概念含义和概念之间的内在关联,已成为词语语义相似度研究的基础。
目前,基于本体的语义相似度计算方法研究已经形成了丰富的研究成果,如表1所示,因此,对其进行系统的梳理显得十分必要。
 | 表1 三个数据库的检索结果 |
2 基于本体的语义相似度计算内涵和影响因素
2.1 基于本体的语义相似度计算内涵
(1)语义相似度与语义距离
语义相似度和语义距离之间存在着密切的关系[ 3]:两个词语的语义距离越大,其相似度越低;反之,两个词语的语义距离越小,其相似度越大。对于两个词语w1和w2,记Sim(w1, w2)为其相似度,Dis(w1, w2)为词语语义距离,则Sim(w1, w2)和Dis(w1, w2)存在下列对应关系:Dis(w1, w2)和Sim(w1, w2)成反向关系,即Dis(w1, w2)越大,则Sim(w1, w2)越小:
①当Dis(w1, w2)为0时,Sim(w1, w2)为1,表示两个词语完全相似;
②当Dis(w1, w2)为无穷大时,Sim(w1, w2)为0,表示两个词语完全不相似或不相关。
两者之间的对应关系可通过下列公式来揭示:
Sim(w1,w2)=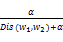
其中,α为调节因子。
(2)基于本体的语义相似度计算思想
词语语义距离的计算方法基本上可以分为两类[ 3]:基于某种世界知识的计算方法和基于大规模语料库的统计计算方法。
基于世界知识计算方法的基本思想是:按照概念间结构层次关系组织的语义词典所包含的概念之间上下位关系和同位关系来计算词语的相似度。该算法依赖于如下的假设:两个词语具有一定的语义相关性,当且仅当其在概念结构层次网络图中存在一条通路。基于公式(1),设C是本体中的概念词集合,词语w1和w2在某种映射算法或映射规则下被映射成概念词c1和c2(c1,c2∈C),那么,词语w1和w2之间的语义相似度计算就可以转换成概念词c1和c2间的相似度计算,Sim(w1,w2)和Dis(w1,w2)可分别表示为Sim(c1,c2)和Dis(c1,c2),其中Sim(c1,c2)∈[0,1],Dis(c1,c2)∈[0,∞)。基于本体的语义相似度计算就属于此类。
基于大规模语料进行统计,主要将上下文信息的概率分布作为词汇语义相似度的参照。其假设前提是:两个词汇具有某种程度的语义相似,当且仅当它们出现在相同的上下文中。
2.2 本体中影响语义相似度计算的主要因素
本体概念体系可用层次树来描述,其中节点表示本体中的概念词;边表示本体中概念词与概念词之间的关系。一般来讲,概念范畴较广的概念词在树中的位置一般比较高,周围节点密度相对较少;概念范畴较为具体的概念词在树中的位置相对较低,且周围节点密度相对较大。因此,树中概念词间语义相似度计算主要受以下因素影响[ 4, 5, 6]:
(1)被比较概念词在本体层次树中所处的深度。在本体层次树中,概念词所处层次越高,越抽象;所处层次越低,越具体。高层次的概念词间的语义相似度一般小于低层次概念词间的语义相似度。因此,路径相同的两个节点,高层次节点所表征的语义距离要大于低层次节点所表征的语义距离。
(2)被比较概念词在本体层次树中所处区域的密度。在本体层次树中,局部区域密度越大,说明该区域对节点概念的细化程度也越大。因此,对组成被比较概念词连接路径的各个边来说,其在本体层次树中所处的密度越大,对应的权重也应该越大。
(3)被比较概念词连通路径上各个边的类型。在本体中,不同的概念关系所表征的语义相似度是不同的。例如,“同义关系”所表征的语义相似度应大于“整体-部分关系”所表征的语义相似度。
(4)被比较概念词连通路径上各个边在本体层次树中的关联强度。在本体层次树中,一个节点可能与多个节点相连接,但这些节点的重要程度通常存在差异,因此,相应的连接边对语义相似度的影响也必然不同。
(5)被比较概念词连通路径上各个边的两端节点概念词的属性。本体,尤其是领域本体,不仅会对概念及其关系进行准确定义,还会对概念的属性进行详细描述。如果某条边两端的概念词所用的相同属性越多,那么其对语义相似度的影响也越大。
3 国内外的相关研究
3.1 国外经典计算模型
学者们一般将基于本体的语义相似度计算方法划分为4类[ 1, 4]:基于距离的语义相似度计算(Edge Counting Measures)、基于内容的语义相似度计算(Information Content Measures)、基于属性的语义相似度计算(Feature-based Measures)和混合式语义相似度计算 (Hybrid Measures)。在不作具体说明情况下,本文介绍的4类算法都是建立在“IS-A”关系树状分类体系基础上的。
(1) 基于距离的语义相似度计算
基于距离的语义相似度计算的基本思想是通过两个概念词在本体树状分类体系中的路径长度量化它们之间的语义距离[ 7]。代表算法有:Shortest Path法、Weighted Links法、Wu and Palmer法、Li et al法、Leacock and Chodorow法等。
Shortest Path法[ 8]认为概念词间的相似度与其在本体分类体系树中的距离有关。计算公式为:
Sim(c1,c2)=2MAX-L(2)
其中,MAX表示概念词c1和c2在分类体系中的最大路径,L表示概念词c1和c2间的最短路径。该算法是现有算法中计算复杂性最小的,不过其主要缺陷是假设本体分类体系中所有边的距离同等重要。显然,该假设并不成立,边的重要性受其位置信息、自身的类型和所表征的关联强度等因素影响。
Weighted Links法[ 9]基于权重的思想对Shortest Path法进行了扩展,考虑到概念词在本体层次树中的位置信息(所在深度和所处区域的密度)和边所表征的关联强度,通过将组成c1和c2连通路径的各个边的权值相加,而不是简单统计两个概念词间边的数量,来计算两个概念词的距离。
Wu and Palmer法[ 10],与Shortest Path法和Weighted Links法不同,并不是通过直接计算c1和c2间的路径长度来计算它们之间相似度,而是基于它们与其最近公共父节点概念词c(Most Common Parent Concept)的位置关系。在本体分类体系树中,两个概念词间必然存在公共祖先节点(如根节点),且可能路径不止一条。最近公共父节点c是与概念词c1和c2间以最少的“IS-A关系”边相关联的公共父节点。计算公式为:
Sim(c1,c2)=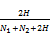
其中,N1和N2分别表示概念词c1,c2与最近公共父节点概念词c间的最短路径,H表示从c到根节点的最短路径。
实践中,信息用户对词语相似度值的比较判断是介于“完全相似”和“完全不相似”间的一个具体值,而从“无限值”到“有限值”的转换是非线性的。Li et al法正是在此基础上提出的[ 1, 11]。该算法模型同时考虑了c1和c2间的最短路径L和最近公共父节点概念词c在分类体系树中所处的深度H,是个非线性函数。计算公式为:
Sim(c1,c2)=e-αL·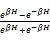
其中,α≥0,β≥0,用以衡量L和H贡献度的参数。文献[12]表明,最佳参数值为α=0.2,β=0.6。
Leacock和Chodorow[ 13]则还考虑了本体分类体系树自身的深度对被比较概念词相似度的影响,他们提出了如下计算模型:
Sim(c1,c2)=-log(length/(2·D)) (5)
其中,Length=N1+N2,N1和N2分别表示概念词c1,c2与最近公共父节点概念词c间的最短路径,D表示c1,c2所在本体层次树的最大深度(当不止有一棵本体分类体系树时,如MeSH主题词表,找出所有包括c1,c2和c的分类体系树,然后取最大分类体系树的最大深度)。
与上述算法模型相比,Hirst-St-Onge法[ 14]认为,如果概念词c1和c2间存在一条较短的路径,且在遍历过程中改变路径方向的次数较少,那么这两个概念词语义相关。计算公式为:
Sim(c1,c2)=C-L-kd(6)
其中,C和k是常量,L表示c1和c2间最短路径长度,d表示遍历过程中改变路径方向的次数。虽然Hirst- St-Onge法开辟了一个新的视角,即考虑到“方向”问题,但由于其在很大程度上取决于“迷航的倾向度”(Tendency to Wander)而不是概念关系,结果表现似乎不是很好[ 15]。
(2)基于信息内容的语义相似度计算
基于信息内容的语义相似度计算方法的基本原理是[ 1, 4, 16]:如果两个概念词共享的信息越多,它们之间的语义相似度也就越大;反之,共享的信息越少,相似度也就越小。在本体分类体系树中,每个概念子节点都是对其祖先节点概念的一次细分和具体化,因此,可以通过被比较概念词的公共父节点概念词所包含的信息内容来衡量它们之间的相似度。
记C为某本体分类体系树中所有概念词的集合,p(c)为实例概念词c出现的概率,ic(c)为实例概念词c所包含的信息内容,则定义[ 4]:
freq(c)=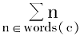
p(c)=freq(c)/N(8)
ic(c)=-ln p(c)(9)
其中,N为C中概念词总数,words(c)表示c所包含的子概念词集合,实例概念词c出现的概率p(c)为其所包含的所有子概念词在分类体系树中出现的频率之和。
根据信息论可知,概念词所包含的信息内容可通过其在给定文献集中出现的频率来衡量,频率越高,信息内容就越丰富;反之,所含的信息内容也就越贫乏。在本体分类体系树中,可以通过子节点概念词的信息内容来计量祖先概念节点的信息内容。
所有基于信息内容的语义相似度计算算法都建立在被比较概念词c1和c2共享父节点所含信息内容基础上。在本体分类体系树中,一个子节点概念词往往对应着多个父节点概念词,因此,比较概念词c1和c2的公共父节点概念词可能不止一个,一般取p值最小(即所含信息内容最多)的那个。记S(c1,c2)为被比较概念词c1和c2的公共父节点概念词集,则
Pmis(c1,c2)= 
Lord等人[ 17]首次提出使用共享父节点所包含的信息内容来计算概念词间的语义相似度。他们直接使用最近公共父节点概念词的p值来计算被比较概念词c1和c2间的相似度。计算公式为:
Sim(c1,c2)=1-pmis(c1,c2) (11)
Resnik[ 16]是第二个使用共享父节点信息内容来计算概念词间的语义相似度,通过p值最小的公共父节点概念词c的信息内容来计算c1和c2间的相似度:
Sim(c1,c2)=-ln pmis(c1,c2)(12)
该方法与Lord等人方法的不同之处在于:一方面它并不是直接使用p值来表征被比较概念词的相似度,另一方面,它并不是基于最近公共父节点的信息内容,而是基于p值最小的公共父节点概念词c的信息内容。
上述两种算法都只考虑了被比较概念词c1和c2的共享信息内容,Lin[ 18]认为还应该考虑c1和c2自身所包含的信息内容,故提出下列语义相似度计算模型:
Sim(c1,c2)=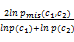
当被比较概念词集属于同一个本体时,使用Lin法可以获得比Resnik法更好的基于相似度的排列结果。
Jiang-Conrath法[ 19]与上述三种算法不同的是:直接通过对语义距离的计算来表征被比较概念词间的相似度。语义距离计算公式为:
Dist(c1,c2)=-2ln pmis(c1,c2)-(ln p(c1)+ln p(c2))(14)
可以看出,和Lin法一样,该算法模型也同时使用了共享父节点和被比较概念词所包含的信息内容。
(3)基于属性的语义相似度计算
事物由其属性特征反映其本身,人们用以辨识或区分该事物的标志就是属性特征[ 20]。事物之间的关联程度与其所具有的公共属性数相关。基于属性的语义相似度计算正是基于此提出的。对于两个被比较概念词而言,公共属性项越多,相似度越大。
Tversky算法模型[ 21]是该类算法的典型,其语义相似度计算模型如下:
Sim(c1,c2)=θf(c1∩c2)-αf(c1-c2)-βf(c2-c1) (15)
其中,θ,α,β,f(c1∩c2)返回的是c1和c2的公共属性数,f(c1-c2)返回的是c1有但c2中没有的属性数,f(c2-c1)返回的是c2有但c1中没有的属性数,参数分别表示c1和c2的公共属性和非公共属性对其相似度计算的影响程度,参数值的确定由具体任务决定,且由于概念词相似度的非对称性,α和β值不一定相同。
该算法既没有考虑被比较概念词在分类体系树中的位置信息,也没有考虑其祖先概念节点和自身所包含的信息内容,只考虑了其属性信息,因此能够很好地利用相应本体的属性集。
(4)混合式语义相似度计算
混合式语义相似度计算方法实际上是对上述三种方法的综合考虑,即同时考虑了概念词的位置信息、边的类型、概念词的属性信息等。代表算法有Rodriguez等人[ 22]和Knappe[ 23]提出的算法模型。其中Rodriguez等人提出的算法模型既可以用来计算单个本体中概念词间的相似度,也可以用来计算多个本体中概念词间的相似度。
Rodriguez et al法[ 22]同时考虑了概念词的位置信息和属性信息,具体包括被比较概念词的同义词集(Synonym Sets)、语义邻节点(Semantic Neighborhoods)和区别特征项(Distinguishing Features)。其算法模型为:
Sim(ap,bq)=wwSw(ap,bq)+wuSu(ap,bq)+wnSn(ap,bq)(16)
其中,ww、wu、wn≥0,分别表示同义词集、特征项、语义邻节点间相似度对整体相似度的贡献大小,且ww+wu+wn=1。ap表示概念词a属于本体p,bq表示概念词b属于本体q。函数Sw,Su和Sn用来计算概念词a和b的同义词集、特征项、语义邻节点间相似度,采用的是Tversky计算模型。该方法也适合跨本体语义相似度计算,是后来跨本体语义相似度计算研究的思想源泉之一[ 24, 25]。
Knappe[ 23]认为,两个概念间可以通过多个路径关联,如果考虑所有的路径,必然会使问题更为复杂。因此,他提出了一种基于共享概念词集(Shared Concepts)的计算模型,在该模型中还引进了复合概念词的概念。一个复合概念词可以分解成多个子概念词。
定义τ(c)为主题词解析器(Term Decomposition),可将概念词c解析成一个概念集S;(c)为向上扩展(Upwards Expansion)函数,可进行概念泛化,泛化结果概念集包含S中所有元素间的IS-A关系链。
记u(c)=(τ(c)),概念词c1和c2向上扩展可获得的公共节点为u(c1)∩u(c2),则Knappe算法模型为:
Sim(c1,c2)=ρ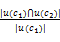
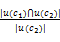
其中,ρ∈[0,1],表征泛化概念的影响程度。该算法模型能满足实际应用中对近似相似度值的需求。
3.2 国内研究概况
基于CNKI和万方数据库中检索到的文献来看,国内在这方面的研究相对较晚,且目前主要成果集中在三个方面:
(1)在对国外上述经典模型进行介绍的基础上进行理论比较或相关改进[ 5, 26],如黄果、周竹荣等人[ 5]提出了一种以Leacock模型为基础,将概念的信息内容和概念的属性作为决策因子的基于领域本体的语义相似度计算模型。
(2)基于通用本体WordNet的词语语义相似度研究,如荀恩东和颜伟[ 3]提出了从WordNet中提取同义词并采取向量空间方法计算英语词语的相似度计算方法。首先从WordNet的Synset、Class Word和Sense Explanation三个集合中抽取出候选同义词并进行特征提取,然后通过计算被比较概念词的各个意义(Sense)在这三个不同意义特征空间中距离来计算意义相似度,最后基于意义相似度来计算词语的相似度。
(3)基于《知网》的中文词语语义相似度研究[ 27, 28]。《知网》中所有描述概念的义原根据上下位关系构成了一个树状层次体系,故可在计算义原相似度的基础上计算词语间的相似度。刘群和李素建[ 27]基于“整体的相似度等于部分相似度加权平均”的思想,提出了基于《知网》的词语语义相似度计算方法,将被比较概念相似度分解成义原相似度的加权组合。
4 结 语
目前,基于本体的相似度计算研究已经取得很多成果,本文仅从算法角度,对国外4类代表算法进行了系统的阐述和比较,并简单综述了国内代表性的研究。基于当前研究成果,笔者认为,今后基于本体的语义相似度研究还需从以下几个方向予以深入[ 24, 29, 30, 31]:
(1)利用本体进行语义相似度计算的前提是要将被比较词语转换成本体中的概念词,因此,准确有效实现被比较词语向本体概念词的映射很重要[ 1]。
(2)网络自身的分布性使得各个领域,甚至是同一个领域,都必然使用自己的本体来描述数据,这就带来了本体异构问题。相似性的度量可以在同一本体内进行,也可以在不同本体内进行。因此,应加强跨本体,尤其是异构本体的语义相似度相关研究。
(3)除了本体的结构信息和被比较概念词在本体中的位置信息,应加强基于本体实例的混合式算法研究,充分利用本体库的统计特性,将两类语义相似度计算方法的特性融合起来。
(4)任何一个本体语义相似度算法都不可能解决所有问题,因此,要加强相似度融合技术研究,如:如何根据具体任务选择调用相关算法和确定相关参数。
(5)在本体体系中,除了“IS-A”纵向分类关系,还包括其他层次关系和各种横向关系;除了相似关系,词语之间的语义关系还包括相关关系。因此,一方面要加强对本体中其他语义关系相似度计算研究,另一方面还应加强相关语义关系相似度计算研究。
此外,基于本体的语义相似度研究决不是某个领域技术或专家能够解决的问题,因此要加强领域之间的合作。
参考文献
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|