对聚类分析中的基本算法K-means算法中的K值确定、初始聚类中心选择以及分类属性数据处理等主要问题进行综述,理清K-means算法的整个发展脉络及算法研究中的热点和难点,提出改进K-means聚类算法的思路。
The main problems of K-means algorithm which is a basic algorithm in clustering are outlined in this paper, such as determination of the optimal clusters, selection of initial centers, and categorical data clustering, etc. The development, the hot spots and difficulties of this algorithm are clarified, and some ideas are introduced to improve the algorithm efficiency.
聚类分析是数据挖掘中的一种重要的分析方法,它的目标是将数据集合分成若干簇,使得同一簇内的数据点相似度尽可能大,而不同簇间的数据点相似度尽可能小。
聚类算法的研究有着相当长的历史,早在1975年Hartigan就在其专著《Clustering Algorithms》[ 1]中对聚类算法进行了系统的论述。之后,学界陆续提出了多种基于不同思想的聚类算法,主要有基于划分的算法、基于层次的算法、基于密度的算法、基于网格的算法和基于模型的算法等。这些算法都能取得不错的聚类效果,其中应用最多且算法思想较为简单的是基于划分的K-means算法。
本文将对K-means算法在文本聚类研究中的基本问题进行全面的综述,并提出一些改进聚类质量的设想。
1967年,MacQueen提出了K-means算法[ 2],他总结了Cox[ 3]、Fisher[ 4]、 Sebestyen[ 5]等的研究成果,给出了K-means算法的详细步骤,并用数学方法进行了证明。MacQueen的算法思想为:给定n个数据点{x1,x2,…,xn},找到K个聚类中心{a1,a2,…,aK},使得每个数据点与它最近的聚类中心的距离平方和最小,并将这个距离平方和称为目标函数,记为Wn,其数学表达式为:
Wn= 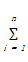
由于K-means算法易于描述,具有时间效率高且适于处理大规模数据等优点,自20世纪70年代以来,该算法在国内外已经被应用到包括自然语言处理、土壤、考古[ 6, 7, 8]等众多领域。在文本聚类领域,K-means算法已经成为基本的算法。随着K-means算法研究的深入,该算法的一些不足纷纷暴露出来,主要包括:需要预先确定K值、会受到初始聚类中心影响、难以处理分类属性数据以及容易收敛于局部最优解等。
K-means算法通过不断地迭代与重新计算聚类中心直至收敛进行聚类,因此聚类收敛条件是算法的重要组成部分。在最初的算法中,MacQueen以平方距离和Wn为目标函数,作为聚类质量的衡量标准,并证明了Wn的收敛性[ 2]。1978年Hartigan[ 9]分析了一维情况下的算法,令K=2,即将全部数据点分割成两个簇,证明了可以用概率收敛点来定义最佳的分割点。Pollard[ 10, 11]考察了多维空间的情况,并将Hartigan的结论推广到多维空间,提出了K-means算法新的聚类质量评价标准,即在保证Wn收敛的同时,还需保证各聚类中心也收敛到最优解。
Creator等[ 12]的研究发现,由于目标函数Wn存在局部极小值点,K-means算法会陷入局部最优解。为了使聚类结果尽量接近全局最优解,需要在算法中加入新的机制,而这些改进都以牺牲目标函数Wn的收敛速度为代价。其中较著名的是1995年Chinrungrueng等[ 13]提出的改进算法,该算法在原有算法中加入了两种新的机制,分别是:允许算法在自适应过程中摆脱目标函数Wn的干扰;采用反馈方式,根据当前聚类质量动态地调整算法的收敛速度。
由于Wn计算的是所有数据点到其聚类中心的距离平方和,因而事实上其反映的仅仅是类内距离的度量,而根据聚类算法的基本思想,即聚类算法应使聚簇内相似度尽可能大,而聚簇间相似度尽可能小的基本原则,聚类收敛函数应该综合考虑类内距离和类间距离。为此,学界提出了很多改进的聚类收敛函数,以期更加全面地反映聚类的质量。其中大多数的改进都是采用类内紧密性(Within-cluster Scatter)与类间分散性(Between-cluster Separation)的比值来作为收敛函数,这样当收敛函数收敛到极小值时,类内紧密性和类间分散性都可以达到较优值。著名的Davies-Bouldin指数(DBI)[ 14]和Dunn指数(DI)[ 15]都是采用这种思想,Davies-Bouldin指数是计算类内距离之和与类间距离之和的比值,而Dunn指数是计算类内距离和类间距离的最值之比。
和很多聚类算法一样,K-means算法需要事先确定K值,K值的选取很大程度上会影响算法的性能。Rezaee等[ 16]根据经验规律认为最佳的聚类数应该在2与 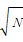
(1)基于聚类有效性函数的解决方法
基于聚类有效性函数的解决方法是一种十分简单的解决方法,通过在[2, 
经典的K-means算法所选用的聚类有效性函数是Wn指数,在此基础上许多学者提出了改进,学界公认较优秀的有MH指数[ 17]、DB指数[ 14]、Dunn指数[ 15]、Generalization of Dunn’s Index[ 18]等。
在国内,许多学者也按照这种思想提出了一系列的解决方法。李永森等[ 19]提出的距离代价函数综合了类间距离和类内距离两项距离函数,类间距离为所有聚类中心到全域数据中心的距离和。类内距离即所有类中对象到其聚类中心的距离之和。作者证明了当距离代价函数取得最小值时,此时对应的K值为最佳聚类数。
张逸清等[ 20]在K-means算法的目标函数中加入一个新的数据项。该数据项用于衡量其他邻近聚类中心与当前聚类中心的距离平方和,并引入一个权值λ,用于调节新数据项在整个目标函数中所占的比例。当算法初始K值过大时,在聚类算法的前期训练中,新数据项的引入就可以使得聚类中心彼此靠近,然后考察聚类中心两两之间的距离值,若小于设定阈值,则将其合并,这样得到的K值更加接近最优解。
张忠平等[ 21]提出了一种基于二分均值聚类的K值决定方法。算法思想为:首先设定两个阈值:簇内相似度λ和簇间相似度γ;在整个数据集上运行二分K均值聚类算法,得到两个类C1和C2,考察C1和C2的簇内相似度,若大于阈值λ,则继续运行二分K均值聚类算法,不断迭代以上过程,最终得到所有的类簇内相似度都小于λ;计算所有类的簇间相似度,将簇间相似度小于γ的类合并,最终得到的类的个数即为K值。该算法思想比较简单,通过两步分裂和合并的过程,得到较好的K值。算法中最重要的问题是确定阈值λ和γ值,这两个阈值决定了数据分裂和合并的效果。作者采用了概率统计的方法确定λ值,计算文本集中两两文本之间相似度的均值μ和标准差σ,并根据实际应用中对簇内相似度的要求给出了一个系数θ,从而可以利用公式λ=μ+θ×σ计算出较优的λ值。在确定另一个阈值γ时,通过实验证明了γ=0.6λ时,合并的效果最好。
(2)基于遗传算法的解决方法
遗传算法在K值选择的研究中也得到了学者的重视。Bandyopadhyay等[ 22]提出了基于遗传算法的GCUK算法。该算法的染色体采用字符串方式编码,即将每一个初始聚类中心的坐标按顺序编码,没有作为初始聚类中心的数据点则以符号“#”表示,编码完成后在逐代交叉中最终得到最佳的K值。该算法的缺点是染色体的字符串表示方法大大增加了算法的开销。为了解决该问题,Lin等[ 23]采用了二进制方式进行染色体编码。该编码方案采用染色体长度作为数据集的大小,被选为初始聚类中心的数据点编码为1,否则为0。
Liu等[ 24]在此基础上提出了AGCUK算法,在染色体编码时为每一个染色体选用K×m个基因(K为随机选取的聚类数目,m为数据点的维度),前m个基因表示第一个初始聚类中心的坐标,接着m个基因表示第二个初始聚类中心的坐标,以此类推完成编码,通过染色体的逐代交叉动态改变K值,此外,在遗传过程中算法还运用了最佳个体保留法,把具有最高适应度的个体不经交叉直接遗传到下一代,最终即可得到最佳的K值。
而巩敦卫等[ 25]在Merwe等[ 26]、Omran等[ 27]的研究基础上提出了一种基于微粒群的优化算法。微粒群优化算法是一种群智能优化算法,其算法思想类似于遗传算法,由Merwe等[ 26]首次将其运用于聚类。基于微粒群优化K值的K-means算法为:首先初始化微粒群,随机产生一个K值,这个K值在[2, 
(3)其他解决方法
Xu等[ 28, 29]提出了RPCL原则,该原则可以在聚类过程中自动确定适当的K值。其主要思想是:对于每个输入而言,对获胜单元的权值予以修正以适应输入值,同时对次胜单元进行惩罚,使之远离输入值。这样经过多次竞争学习之后,就可以使权值向量趋向于聚类中心。
Pelleg等[ 30]提出了X-means算法用于解决K值选定的问题。算法的主要步骤为:首先通过经典的K-means算法对数据集聚类,得到K个聚类中心;对聚类所得的K个类逐个进行聚类,再运用贝叶斯信息标准(BIC)进行判断,如果BIC标准得分更高,则采用新的聚类中心,否则回到原来的聚类,算法经过O(K)的时间开销,就可以寻找到最佳的K值。
综合上述研究可以发现,学界已经提出了多种K值选取方法,并分别基于不同的思想。基于聚类有效性函数的解决方法算法思想简单,但是需要付出较大的时间开销,遗传算法作为一种优秀的优化算法,应用于K值的确定是十分有效的。目前,多种K值确定算法都运用了遗传算法或者类似于遗传算法的方法,这些算法聚类效果的优劣取决于染色体的编码方式,在编码时既需要兼顾进化速度,又需要保证得到令人满意的进化结果。RPCL算法通过吸引竞争获胜者,并推开次胜者的方法确定聚类中心和K值,目前已经比较成熟,在文本聚类中应用广泛。其他的如X-means等算法的聚类效果也都得到了实验结果的证明。
在K-means算法中,初始聚类中心是随机选取的,因此可能造成在同一类别的样本被强行当作两个类的初始聚类中心,使聚类结果最终只能收敛于局部最优解,因此K-means算法的聚类效果在很大程度上依赖于初始聚类中心的选择。针对该问题,学界提出了多种改进的算法。
Duda等[ 31]在实现K-means算法时采用了最简单的解决办法,即进行多次初始聚类中心的选择并聚类,从中找到最优解。该解决办法思想非常简单,但在数据量较大时实用价值不大。
(1) 基于密度的解决方法
基于密度的初始聚类中心选择方法是根据聚类对象数据点的密度分布情况选择初始聚类中心,这样可以很好地避免初始聚类中心过于密集的情况发生。基于密度的解决方法有许多种,其中具有代表性的有:
①1994年,Katsavounidis等[ 32]提出一种简单的解决方法,即尽可能分散初始聚类中心,算法思想为:D为数据集,C为初始聚类中心集合,先选择D边界上的点c1作为第一个聚类中心,加入集合C中,然后使用距离c1最远的点c2作为第二个聚类中心,也加入集合C中。
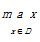
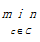
随后迭代计算式(2)的值,选择符合条件的点作为初始聚类中心。事实上,式(2)就是计算空间中的每个点与已经被选取的聚类中心的距离,找出离该点最近的聚类中心,然后比较它们与最近聚类中心的距离,选出距离最大的点作为聚类中心。
②2004年,Khan等[ 33]提出了CCIA算法,其主要思想是利用数据点的均值、标准差、百分位数等统计信息提供数据点的密度分布信息,可以得到m个描述数据的标签信息,在标签上进行聚类得到K’(K’>K)个聚类中心,然后进行合并,从而得到初始聚类中心,通过在多个数据集上的实验,证明了CCIA算法的优越性。
③2007年,Redmond等[ 34]提出了另一种基于密度的解决办法,即通过构建Kd-tree得到数据集的密度分布,然后利用密度信息,采用类似于Katsavounidis等[ 32]的算法得到初始聚类中心。
④2006年,张文君等[ 35]提出的算法类似于CCIA[ 33],其思想为:若K-means算法的初始聚类中心分布在点密度较大区域,则能获得更好的收敛速度和聚类效果,因此利用聚类数据的均值标准差与数据分布的关系则可得到更好的初始聚类中心选取方法。
⑤2007年,牛琨等[ 36]提出了基于密度指针的初始聚类中心选择算法DP。DP 算法以网格单元的几何中心为对称中心,连接该中心与网格单元各顶点,形成超三角形子空间;进而根据各超三角形子空间与邻居单元相邻的超三角形子空间的密度差异确定密度指针的方向,并根据密度指针计算出每个密集网格单元的聚集因子;最后将具有较大局部聚集因子的网格单元簇的重心作为初始聚类中心。
⑥2010年,张文明等[ 37]提出的文本聚类初始中心选择算法的思想是:给定阈值R、t,对于文本集中任意一个文本p,如果在半径R的邻域之内只有自身一个文本,则将该文本加入候选参考集。如果在半径R的邻域之内含有不少于t个文本,则称p为核心文本,将p的R邻域内的所有文本的均值加入候选参考集。这样就可得到候选参考集S{S1,S2,…,Sj},如果j大于设定的聚类数K,则将候选参考集中最相似的两个文本删除,将其均值放入候选参考集。如果j小于设定的聚类数K,则重新设定阈值R、t的值。通过三组实验,结果表明该算法在聚类效果和稳定性方面都有了一定的提高。
(2) 基于优化算法的解决方法
随着研究的深入,许多优化算法也被应用于初始聚类中心的选择。其中模拟退火算法以其高效的寻优效率被广泛应用。模拟退火算法是模拟物理学上固体退火过程的一种寻优算法,最早由Metropolis等[ 38]在1953年提出。20世纪80年代,模拟退火算法被应用到组合优化问题,算法思想为:先设定一个初始解X作为当前解,并设定初始温度C作为控制参数;然后在当前解的邻域中随机产生一个新解X’,计算转移概率,如果新解优于当前解,则置转移概率为1,如果新解劣于当前解,则赋予一定的转移概率,转移概率的计算公式为exp(-(f(X’)-f(X))/C),不断迭代以上过程,最终以概率1得到全局最优。由于模拟退火算法在优化过程中允许目标函数以一定的概率恶化,因此可以避免其他算法容易陷入局部最优解的问题。1989年,Klein等[ 39]进行了实证研究,对模拟退火算法和经典K-means算法的聚类效果进行了比较,结果表明模拟退火算法获得了较好的聚类效果,但是算法的时间复杂度增加明显。2009年,Dong等[ 40]先通过二分K-means算法将数据集分为K个大类,再利用模拟退火算法优化聚类中心,提高了聚类的准确度。
和模拟退火算法一样,遗传算法也被应用于初始聚类中心的优化。1991年,Bhuyan等[ 41]提出可以用遗传算法改进聚类效果,随后Jones等[ 42],Babu等[ 43]也相继提出应用遗传算法改进K-means算法初始聚类中心的思路。基于此,1999年,Krishna等[ 44]提出GKA算法(Genetic K-means Algorithm)。在此前的算法中,染色体交叉和适应度计算存在一个矛盾,即优化一方的计算复杂度会影响到另一方的速度,而GKA算法采取了效率更高的染色体编码方案解决了该问题。2000年,Maulik等[ 45]在多个人工数据集和现实数据集中对应用遗传算法优化后的K-means算法进行了测试,得到了明显优于传统K-means算法的聚类效果。2007年,Laszlo等[ 46]采用了新的交叉算子改进了该算法,实验结果证明,在基准测试程序和大规模数据集上,都得到了更优的实验效果。
(3)其他解决方法
除了上述方法外,国内外学者还提出了一些其他的解决方法,都取得了良好的聚类效果。
1998年,Bradley等[ 47]提出了RA(Refinement Algorithm)算法,其主要思想是将原始数据集分为J个子集,运用K-meansMod算法对J个子集进行聚类,(K-meansMod算法是Bradley等对K-means算法的修改,主要的不同在于对空类的处理),得到聚类中心集,共J×K个点,再分别对这J×K个点运用K-means算法,得到的K个类中心作为最终初始聚类中心。
2001年,Bandyopadhyay等[ 48]提出了SAKM聚类算法,算法综合了模拟退火算法的寻优能力和K-means算法的搜索能力,在聚类过程中不再采用确定性的聚类方式,而是根据数据点离聚类中心的距离赋予数据点一定的转移概率,最终完成聚类。
2008年,Zalik[ 49]提出的算法很好地解决了K-means算法的两个问题:K值和初始聚类中心的选择。即构建一个耗损函数,通过两步使得函数取得全局最小值,第一步通过初始聚类给每一个类赋予至少一个聚类中心,第二步在迭代中算法自动惩罚可能获胜的非全局最优点,最终通过调整聚类中心使得耗损函数最小化。当耗损函数取得最小值时,正确的聚类数K值和初始聚类中心也就同时确定。
2010年,Cao等[ 50]提出利用数据点的邻居信息来确定初始聚类中心的方法。首先通过设定阈值ε,将距离小于ε的两个点视为邻居点。利用数据点的邻居信息计算得到每个数据点的凝聚度,凝聚度的值越大,则该数据点的邻居集出现在类别分界的个数越少,因而该数据点更应该被选为初始聚类中心。通过与其他三种初始聚类中心选取算法的对比证明了该算法在聚类效果和时间复杂度上的优越性。
2004年,刘立平等[ 51]在RA算法基础上提出了一种新的初始聚类中心选择方法,算法思想为:首先从原始数据集中抽取一个样本集,在样本集中随机选择pK个(p为常数)初始聚类中心,运用K-means算法得到pK个类。去除较小的类,对剩余的类运用聚类算法聚成K个类,得到K个聚类中心,再选用离这些聚类中心最近的数据点作为初始聚类中心。算法通过两步聚类保证初始聚类中心分别属于不同的类,经过实验证明比RA算法具有更好的聚类效果。
2005年,王汉芝等[ 52]利用超立方体技术,首先将数据中心划分为几个区间,并计算每个区间的超立方体编码,再利用超立方体编码计算K-means算法的初始聚类中心。
自Creator等[ 12]发现K-means算法会受到初始聚类中心的影响而收敛于局部最优解的问题之后,初始聚类中心的选择就一直是K-means算法的研究热点。上述研究中的解决方案各有优缺点,基于密度的方法根据数据点的密度信息使得初始聚类中心尽可能分散开来,一定程度上缓解了局部最优解问题,但是却难以做到进一步的优化。利用模拟退火算法和遗传算法这样的优化算法对初始聚类中心进行优化是目前学界研究的热点。相比确定K值,优化算法应用于初始聚类中心的选择更加合适,目前已经提出了许多比较成熟的算法,并且已经有相关的专著问世[ 53]。值得一提的是,该方向国内的许多研究成果也十分出色,如王汉芝、牛琨等学者的研究。
传统的K-means算法只适用于处理数值属性的数据,而对于分类属性和混合属性数据集则不太适用。围绕该问题,国外学者提出了众多解决方法,1995年Ralambondrainy[ 54]提出将分类属性转化为多个取值为0 和1 的数值属性,再运用K-means 算法的思路;1997年、1998年Huang[ 55, 56]分别提出了适用于纯分类属性数据集的K-modes算法和适用于混合属性数据集的K-prototypes算法。
(1)K-modes算法
K-modes算法针对分类数据的特点引入Modes的概念来代替原有算法中的聚类中心Means。首先给出分类数据之间的距离度量方法,数据点X(x1,x2,…,xj)和Y(y1,y2,…,yj)之间的距离定义为:
d(X,Y)= 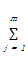
其中函数δ定义为:
δ(xj,yj)=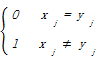
Modes的定义为:给定任意的分类数据集X(X1,X2,…,Xn),都有m个分类属性A{A1,A2,…,Am},使得Xi取得集合A中的一个分类,那么分类数据集X的Modes(记为Q),Q{q1,q2,…,qm}使得目标函数D(Q,X)取得最小值。
D(Q,X)= 
K-modes算法是K-means算法在分类数据集应用上的扩展。相比其他解决方法,K-modes算法无需对分类数据进行变换,Huang通过在大豆疾病数据集和健康保险数据集上的实验证明了K-modes优秀的收敛速度和聚类性能。
(2)K-prototypes算法
K-prototypes算法是在K-means和K-modes算法的基础上提出的,用于处理混合属性数据集。与K-modes算法一样,Huang还首先给出了混合属性情况下数据点之间的距离度量方法,对于两个混合属性对象集X,Y,设前p个数据点为数值属性,后面为分类属性。则距离度量公式为:
d2(X,Y)= 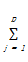
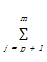
随后也相应地对聚类目标函数进行了改写:
P(W,Q)= 
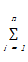
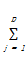
+γ 

K-prototypes算法就是要找到最佳的Q,使得目标函数P(W,Q)取得最小值。
除了K-modes和K-prototypes算法以外,Chaturvedi等[ 57]在2001年也提出了一项面向分类数据集的K-modes-CGC算法。Huang[ 58]在后期的研究中证明了K-modes-CGC算法与原始的K-modes算法是等价的。
K-modes和K-prototypes算法很好地解决了K-means算法在处理分类数据集和混合数据集上的不足。但是,与K-means算法一样,K-modes算法也需要预先设定初始Modes,这样算法会受到初始Modes的影响而收敛于一个局部最优解。基于这个问题,Sun等[ 59]在2002年提出应用迭代初始点求精算法得到初始Modes,再应用K-modes算法,该算法得到了比普通K-modes算法更好的聚类效果。
(3)K-summary算法
2006年,蒋盛益等[ 60]针对K-modes算法的不足提出了K-summary算法,认为K-modes算法采用Modes来表示类的对应“中心”,难以准确反映类中对象的取值情况,会导致距离计算不够精确,从而影响聚类质量。因此,他们提出用摘要信息CSI(Cluster Summary Information)来表示一个类,CSI包括集合{n,Summary}中两项信息,n表示类大小,Summary则由分类属性中不同取值的频度信息和数值型属性的质心两部分组成。同时提出了一套与CSI配套的距离计算方法,适用于混合属性数据集。
K-summary算法的步骤类似于K-means算法:先通过初始化,选择k个初始点构造初始的类CSI,再将数据集中的每个点划分到最近的类中,更新类CSI的值,迭代以上过程,直到算法收敛。
采用大豆疾病等5个数据集进行测试,结果表明,相比K-modes和K-prototypes算法,K-summary算法取得了更好的聚类效果,但是需要付出更大的时间和空间开销。
除了提到的三种算法以外,2010年,Roy等[ 61]还提出了基于遗传算法的混合属性数据聚类K-means算法,采用新的染色体编码方案和适应度计算方法解决了混合属性数据的相似度计算问题。这些算法的提出使得K-means算法具备了处理分类属性以及混合属性数据的能力,拓展了K-means算法的应用领域。
K-means算法是一种十分优秀的聚类算法,以其简单的算法思想、较快的聚类速度和良好的聚类效果得到了广泛的应用。对于该算法在聚类过程中暴露出的若干问题,本文对其中K值确定、初始聚类中心选择以及分类属性数据处理等主要问题进行了综述。
在K-means算法提出至今的40多年里,大量的研究集中在算法思想上,从而仅仅通过改进算法来大规模提高聚类效果的设想已经变得十分困难,因此需要在其他方向另辟蹊径。比如,在文本聚类领域,基于文献/科学计量学的聚类研究等就取得了不亚于传统聚类算法的聚类效果, 当然这些方法目前还只能应用于一些特殊的聚类领域,缺乏通用性。那么是否可以借鉴文献计量或者科学计量学的研究成果利用文本的其他外部特征为K-means算法中K值选取、初始聚类中心的选择等提供必要的线索信息也是值得情报学研究工作者深入思考的问题,是可以充分发挥本学科优势的地方,也将是作者下一步的研究方向。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
|
| [47] |
|
| [48] |
|
| [49] |
|
| [50] |
|
| [51] |
|
| [52] |
|
| [53] |
|
| [54] |
|
| [55] |
|
| [56] |
|
| [57] |
|
| [58] |
|
| [59] |
|
| [60] |
|
| [61] |
|

