引用本文
俞立平, 潘云涛, 武夷山. 学术期刊非线性评价方法的检验与修正研究* . 现代图书情报技术, 2011, 27(7): 110-115
Yu Liping, Pan Yuntao, Wu Yishan. Study on Testing and Improving Nonlinear Evaluation Methods for Academic Journals. 现代图书情报技术, 2011, 27(7): 110-115  
Permissions
Copyright©2011, 《现代图书情报技术》编辑部
《现代图书情报技术》编辑部版权所有
学术期刊非线性评价方法的检验与修正研究*
俞立平1, 潘云涛2, 武夷山2
1宁波大学商学院 宁波 315211
2中国科学技术信息研究所 北京 100038
基金:*本文系国家社会科学基金后期资助项目“科技评价中多属性评价方法基本理论研究”(项目编号:10FTQ003)的研究成果之一;
摘要

讨论采用非线性评价方法评价可能出现指标值增加、评价值反而下降的异常问题,提出一种新的检验与修正方法——回归调整法,试图从指标选取与非线性评价方法的选择两个方面进行改进。

关键词: 学术期刊; 非线性评价方法; 回归调整法
中图分类号:G304
Study on Testing and Improving Nonlinear Evaluation Methods for Academic Journals
Yu Liping1, Pan Yuntao2, Wu Yishan2
1Business School, Ningbo University, Ningbo 315211, China
2Institute of Scientific & Technical Information of China,Beijing 100038, China
Fund:
Abstract

In nonlinear evaluation, sometimes an abnormal phenomenon occurs where the final evaluation score decreases while the value of component indicators increases. Regression adjustment method, a new method for test and improvement, is suggested as a solution to the above abnormality.

Keyword: Academic journals; Nonlinear evaluation; Regression adjustment method
1 引言

学术期刊是一个国家和地区科技创新水平的重要窗口,是知识创新、科技成果转化为生产力的重要桥梁,在推动社会科技进步方面发挥着不可替代的作用。期刊定量评价方法包括单指标评价、多指标综合评价两大类。国外学者在期刊评价中设计了各种各样的指标。传统的指标相对单一,包含的信息量较少,如影响因子、被引半衰期、基金论文比等。后来发展到一些复合指标,包含的信息量较大,典型的有FC 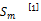、H指数[ 2]、ACIF[ 3]等。

由于单指标评价方法提供的信息量有限,因此多指标综合评价方法(也称为多属性评价)得到了广泛的应用。多指标综合评价方法又可以进一步分为两大类:

(1)线性评价方法,其基本原理是对评价指标进行主客观赋权,然后将数据标准化后加权汇总,评价结果与指标值之间的关系是线性的。如专家会议法、德尔菲法、层次分析法、熵权法、变异系数法等。

(2)非线性评价方法,主要指运用运筹学、模糊数学、系统工程等领域的方法进行评价,评价值与指标值之间的关系是非线性的。一些系统评价方法无须赋权,如主成分分析法、数据包络分析、TOPSIS法等;另一些系统评价方法也可以赋权,采用主客观赋权方法均可,但一般以主观赋权为主,如加权TOPSIS法、ELECTRE法、模糊综合评价法、PROMETHEE等。

虽然各种评价方法都有一定的特点和适用范围,如主成分分析和因子分析比较适合于指标间相关程度较高的评价;数据包络分析(DEA)适合于有投入产出指标的评价,总体上,很多评价方法(如TOPSIS法、熵权法、灰色关联法等)的适用性都是比较广泛的,导致对于学术期刊评价而言,客观上可以采用许多种评价方法,因此也就带来针对同一评价对象,不同评价方法的评价结果不尽相同的现象。由此引出两个问题:评价方法的选择问题;评价方法的检验和修正问题。对于线性评价方法,主要是根据不同评价原理进行方法的选择;对于非线性评价方法,既存在根据评价原理选择评价方法的问题,也存在对评价方法本身的检验和修正问题。

本文重点讨论非线性评价方法的检验与修正问题,以中国科学技术信息研究所医学期刊评价数据为例,提出了一种解决该类问题的系统方法——回归调整法(Regression Adjustment Method)。以主成分分析法为例,首先用主成分分析进行评价,然后对评价结果进行回归分析,发现存在的问题,并进行相应的判断与修正。

2 文献综述

国内外学者在该领域进行了大量广泛的研究。在多指标综合评价领域,学者们采取不同的方法进行学术期刊评价。庞景安等[ 4]及李凯扬等[ 5]利用层次分析法对期刊进行评价。王玖等[ 6]运用秩和比法进行医学学术期刊学术质量综合评价。王小唯等[ 7]将期刊以往状态的评价结果作为各期刊基础条件的一种度量,再运用DEA方法测算出它们的二次相对评价值。邱均平等[ 8]提出了期刊评价指标体系的三维层次结构图,并利用灰色关联法进行评价。Yue 等[ 9]利用结构方程的原理建立了一个期刊影响力的分析框架,但没有进行实证。陈汉忠[ 10]应用主成分分析对学术期刊进行评价。凌春艳等[ 11]提出自然科学学术期刊质量指标体系的属性数学综合评价模型并进行了评价。苏新宁[ 12]采用指标体系赋权进行中国人文社会科学期刊的评价。李修杰等[ 13]运用判别分析法建立了期刊评估指标体系。从目前的科技评价现状看,广大学者采用各种不同的评价方法进行学术期刊评价,同时涌现出不少成果,既采用线性评价方法,也采用非线性评价方法。

俞立平[ 14]在研究中发现,主成分分析评价存在一个问题,就是当期刊的某个正向指标值增加时,有可能出现评价值反而减小的情形。苏为华[ 15]认为,为解决主成分分析中的权重为负问题,如果指标本身并非不合理,则应采用非约束主成分进行评价,或者干脆不采用主成分分析进行评价。侯文[ 16]在主成分分析中发现,第一主成分中存在某些指标系数为负的状况,这与评价的实际意义不符,提出了采用分组主成分分析来进行修正。总之,现有的研究仅局限于指出主成分分析存在的问题,并没有提出较好的解决问题的办法,极少有学者将问题推广到非线性评价方法的共性问题来进行深入研究。

3 研究方法
3.1 主成分分析

主成分分析由Pearson[ 17]首先提出,它将原来指标重新组合成一组新的互相无关的几个综合指标来代替原来指标,同时根据实际需要从中选取几个较少的综合指标尽可能多地反映原来指标的信息。主成分分析常被用来作为寻找判断某种事物或现象的综合指标,并且给综合指标所包含的信息以合适的解释,从而更加深刻地揭示事物的内在规律。

3.2 多元线性回归分析

为了分析非线性评价结果与各指标间的关系,采用常见的多元线性回归模型进行分析。 F.Gallton较早采用回归模型研究儿子的身高和父亲的关系[ 18],其基本形式如下:

Y=a1X1+a2X2+…+anXn (1)

其中,Y为评价值,用其作为被解释变量;X1,X2…Xn为期刊评价指标,即解释变量;a1,a2…an为系数,实际上该系数反映了各指标的贡献大小,某种程度上相当于权重。如果系数为正,说明该指标增加会带来评价得分的增加,对于正向指标而言,这是正常的。一旦正向指标的系数为负数,显然就存在问题。采用多元回归的目的,就是为了发现类似的问题。

3.3 多重共线性检验

多重共线性是指线性回归模型中的若干解释变量或全部解释变量的样本观测值之间具有某种线性关系。多重共线性可分为完全和不完全多重共线性两种情况,一般后者居多。

Gujarati[ 19]认为多重共线性会导致R2值较大并且t检验值较小、方差和标准差都很大、回归系数符号有误等问题。实践中,常用容限度(Tolerance)和方差扩大因子(Variance Inflation Factor,VIF)来检验多重共线性。

容限度和方差扩大因子是检验多重共线性的两个重要指标。容限度等于1减去每个自变量Xj作为因变量对其他自变量回归时得到的R2,即:

Tolerance=1-

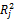(2)

容限度很大时,Rj很小,说明Xj 包含的独立信息很多,可能成为重要解释变量;反之,容限度很小,Rj很大,说明Xj 与其他自变量的信息重复性越大,对因变量Y 的解释能力越小,容易出现多重共线性。容限度的大小是根据研究者的具体需要制定的,通常当容限度小于0.1时,便认为变量Xj 与其他变量之间的多重共线性超过了容许界限。

方差扩大因子是容限度的倒数,即:

VIF=

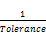(3)
=

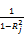
当容限度为0.1 时,VIF为10。通常当VIF> 10 时,便认为变量Xj 与其他变量之间存在多重共线性。

3.4 岭回归

一旦发生多重共线性,传统的做法是采取逐步回归法删去相关变量,必然会带来被删变量数据信息的丢失,最好的消除多重共线性的方法是采取岭回归法。岭回归(Ridge Regression)实际上是一种改良的最小二乘法,是一种专门用于共线性数据分析的有偏估计回归方法。Horel等[ 20]提出了岭回归估计方法,该方法放弃最小二乘的无偏性,损失部分信息,以放弃部分精确度为代价来寻求效果稍差但更符合实际的回归方程。

经典的回归是计算:

=(X'X)-1X'y (4)

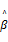
存在的问题是当数据存在多重共线性的时候,矩阵X’X 几乎是奇异(Singular)的,会导致最后估计结果的方差非常高。可以通过变换矩阵的特征值来规避这个问题:

=(X'X+kI)-1X'y (5)

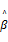
这样会减少估计的方差,但这样的估计是有偏的(Biased),如果减少的方差远远高于增加的估计偏差,均方误差(Mean Square Error,MSE)会减少,那么新的方法将是有效的。可以将岭回归看作是一个惩罚回归,用最小化公式:

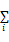(6)
(yi-b0- xijbj)2+k

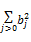
来代替最小化公式:

(yi-b0- xijbj)2 (7)

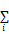
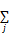
这样能避免很大的方差。加入限制条件 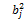≤s,这样问题就变成了选择恰当的k或s,使方差较小并且估计的偏差也较小。可以通过探索法、作图或证明来选择恰当的参数。采用SPSS 17.0可以方便地进行岭回归的估计。

3.5 回归调整法的原理

在用非线性评价类方法进行评价时,可能存在某个正向指标值增加、评价值反而减小的情况。那么究竟是该指标值不合理还是评价方法不合理,对这个问题要进行具体分析。在确认指标选取没有问题的情况下,要分析指标值增加、评价值减小的原因,如果采取岭回归排除多重共线性的影响后,该问题依然存在,那么就要重新选取其他评价方法进行评价;如果评价方法肯定没有问题,采用岭回归排除多重共线性影响后,问题依然存在,则要考虑删除相关指标。与非约束主成分分析法相比,回归调整法是针对非线性评价类方法的一种相对通用的检验方法。

本文提出了学术期刊系统评价方法的检验与修正方法,其步骤是:

(1)选取评价对象,将所有指标进行标准化处理,并将反向指标全部转化为正向指标。

(2)采用某种系统评价方法对学术期刊进行评价。

(3)将评价结果作为因变量,所有评价指标作为自变量进行回归,如果没有指标系数为负的情况,则无须修正(这里放宽了回归系数的统计检验)。

(4)进行多重共线性诊断,如果不存在多重共线性,并且回归系数都大于零,则检验结束。如果有回归系数为负数的情况,则删除相关指标,重新回到步骤(2)。

(5)如果存在多重共线性,则采用岭回归进行估计。如果估计结果回归系数有负数,则删除相关指标,重新回到步骤(2)。

如果岭回归所有回归系数为正数,并且普通回归的所有系数也为正数,则调整结束。

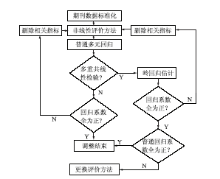
如果岭回归所有回归系数为正数,但是普通回归的系数存在负数,说明出现该负数的原因是多重共线性引起的,此时不能选用该非线性评价方法进行评价,因为会导致指标增加、评价值反而下降的异常情况。此时,可以用岭回归系数作为权重进行评价或者用其他方法进行评价。回归调整法原理如图1所示:

图1 回归调整法原理图

4 变量与数据

本文数据来自于中国科学技术信息研究所CSTPC数据库,以医学类期刊为例进行研究。中国科学技术信息研究所从1987年开始对中国科技人员在国内外发表论文数量和被引情况进行统计分析,并利用统计数据建立了中国科技论文与引文数据库,同时出版《中国学术期刊引证报告2008》[ 21]。本文选取2007年的537种医学类期刊数据,指标有:总被引频次、影响因子、即年指标、他引率、扩散因子、学科影响指标、学科扩散指标、引用半衰期、被引半衰期、基金论文比、平均作者数、平均引文数、地区分布数,共13个。数据描述统计量如表1所示:

表1 数据描述统计量

由于要对期刊进行评价,所以必须对数据进行标准化处理,每项指标最大值设为100,然后按比例进行调整。即:

Xj= 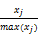×100 (8)

此外,被引半衰期和引用半衰期是两个反向指标,必须进行适当处理,方法是用100减去其标准化后的结果再做一次标准化,这样就变成了正向指标。即:

Xj=100- 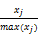×100 (9)

5 实证结果

(1)第一轮处理

在进行主成分分析时,必须首先进行KMO检验与Bartlett检验。 KMO是对样本充分度进行检验的指标,一般要大于0.5。本文采用SPSS进行数据处理,KMO值为0.723>0.5,通过了统计检验;Bartlett值为2 893.908,P<0.000,也通过了统计检验。即期刊评价采用主成分分析的条件全部具备。前6个主成分的累计贡献率为80.20%,因此采用前6个主成分进行评价。

为了对主成分分析评价结果进行检验,将评价结果作为因变量,13个指标作为自变量进行回归,结果如表2的主成分分析回归1所示。拟合优度很好,几乎为1,所有指标的回归系数在1%的水平上通过了统计检验。但是扩散因子、被引半衰期(标准化后已经改为正向指标)、地区分布数的回归系数为负,也就是说,如果用主成分分析进行评价,面临着这三个指标值增加、评价值反而下降的问题,显然有悖于常识。

那么是否存在由于多重共线性引起这三个指标回归系数为负的可能,必须进行多重共线性检验,采用SPSS进行多重共线性检验,结果表明,没有哪个指标的方差扩大因子大于3,因此不存在多重共线性。很显然,选取这三个指标是不合适的。

(2)第二轮处理

删除扩散因子、被引半衰期、地区分布数这三个指标,用10个指标重新进行主成分分析,KMO值为0.712>0.5,Bartlett值为1 716.810,P<0.000,说明可以采用主成分分析进行评价,前5个主成分的累计贡献率为79.47%,采用前5个主成分进行评价。

表2 主成分数据处理结果

将评价结果作为因变量,10个指标作为自变量进行回归,结果如表2主成分分析回归2所示。拟合优度很好,几乎为1,所有指标的回归系数在1%的水平上通过了统计检验。但是引用半衰期回归系数为负(标准化后已经改为正向指标),显然是不合适的。

多重共线性检验结果表明,10个指标的方差扩大因子最大不超过3,不存在多重共线性。很显然,选取引用半衰期指标不合适。

(3)第三轮处理

继续删除引用半衰期指标,利用余下的9个指标进行主成分分析。KMO值为0.704>0.5,Bartlett值为1 644.173,P<0.000,主成分分析的条件具备,前5个主成分的累计贡献率为83.97%,采用前5个主成分进行评价。

将评价结果作为因变量,9个指标作为自变量进行回归,结果如表2主成分分析回归3所示。拟合优度很好,几乎为1,所有指标的回归系数在1%的水平上通过了统计检验。但是即年指标回归系数为负,显然是不合适的。

进行多重共线性检验,结果表明,9个指标的方差扩大因子最大同样不超过3,不存在多重共线性。很显然,选取即年指标不合适。

(4)第四轮处理

删除即年指标,用8个指标作为自变量进行回归,结果如表2主成分分析回归4所示。拟合优度很好,几乎为1,所有指标的回归系数在1%的水平上通过了统计检验。并且所有指标的回归系数均为正数。

继续进行多重共线性检验,结果显示,8个指标的方差扩大因子最大不超过3,不存在多重共线性。至此,整个处理过程结束。

(5)回归调整法

通过回归系数调整,结果表明,对学术期刊进行评价,如果要采用主成分分析,只能选取总被引频次、影响因子、他引率、学科影响指标、学科扩散因子、平均引文数、平均作者数、基金论文比8个指标进行评价,才能保证评价结果的单调性,即指标值增加,评价值提高。

必须对删除的5个指标进行认真分析,如果确实有些指标非常重要,那么不能采用主成分分析进行评价。

还必须考虑到另外一种特殊情况,就是采用回归调整法如果循环较多,仍然不能收敛,即到最后剩下少数几个指标时,回归系数仍然为负,可能已经不能满足主成分分析自身的条件,在这种情况下,也不能采用主成分分析进行评价。

(6)主成分分析最终评价结果

初始拟采取13个指标评价,如果不进行回归调整,那么就是13个指标主成分分析的结果。经过调整,删掉了5个指标,采用主成分分析的结果如表3所示。为了节省篇幅,表3仅给出前20种期刊的评价结果和排序。

6 结语

(1)非线性评价方法隐含的不足必须受到重视。迄今为止,共有几十种非线性评价方法,其原理各不相

表3 部分期刊不同非线性评价排序

同,学者们已经在主成分分析中发现了某个正向指标增加、评价值反而下降的异常情况,其他非线性评价方法中其实有存在类似问题的可能性,但尚未被发现或受到重视。回归调整法作为一种稳健的检验与修正方法,可以广泛适用于所有的非线性评价。

(2)删除指标时要慎重。回归调整法可以作为一种评价指标选取方法。根据某种评价方法的原理,如果某个正向指标增加,反而出现回归系数为负的异常情况,则说明这个指标与其他指标相比,是“特殊的”,这时要认真对该指标进行分析,如果确实不妥,应删除该评价指标。在用回归调整法处理时,如果某些指标非常重要,根本不能删除,则要考虑取消采用该评价方法进行评价。回归调整法某种程度上也可以作为评价指标选取的一种客观方法。

(3)回归调整循环不应过多。通常情况下,采用某种非线性评价方法进行评价,经过一到两轮的回归调整,在删除少数不合适指标后,模型稳定,是可以采用该方法进行评价的。反之,如果经过数轮调整,在删除许多指标后才达到稳定,那么要慎重考虑是否选取该非线性评价方法;如果经过数轮调整仍不能收敛,则不能选取该非线性评价方法进行评价。

参考文献
[1] Moed H F, De Bruin R E, Van Leeuwen T N. New Bibliometric Tools for the Assessment of National Research Performance[J]. Scientometrics, 1995, 33(3): 381-422. [本文引用:1] [JCR: 2.133]
[2] Hirsch J. An Index to Qualify an Individual’s Scientific Research Output[J]. Proceeding of the National Academy of Sciences of the United States of America, 2005, 102(46): 16569-16572. [本文引用:1]
[3] Markpin T, Boonradsamee B, Ruksinsut K, et al. Article-count Impact Factor of Materials Science Journals in SCI Database[J]. Scientometrics, 2008, 75(2): 251-261. [本文引用:1] [JCR: 2.133]
[4] 庞景安, 张玉华, 马峥. 中国科技期刊综合评价指标体系的研究[J]. 中国科技期刊研究, 2000, 11(4): 217-219. [本文引用:1]
[5] 李凯扬, 贾玉萍. 基于AHP的期刊全文数据库的模糊综合评价[J]. 情报科学, 2005, 23(11): 1688-1703. [本文引用:1]
[6] 王玖, 徐天和. 秩和比法在医学科技期刊学术质量综合评价中的应用[J]. 数理医药学杂志, 2003, 16(3): 266-267. [本文引用:1]
[7] 王小唯, 杨波, 潘启树. 学术期刊质量评估的二次相对评价方法[J]. 编辑学报, 2003, 15(3): 231-232. [本文引用:1]
[8] 邱均平, 张荣, 赵蓉英. 期刊评价指标体系及定量方法研究[J]. 现代图书情报技术, 2004(7): 23-26. [本文引用:1]
[9] Yue W, Wilson C S. Measuring the Citation Impact of Research Journals in Clinical Neurology: A Structural Equation Modeling Analysis[J]. Scientometrics, 2004, 60(3): 317-332. [本文引用:1] [JCR: 2.133]
[10] 陈汉忠. 主成分分析在科技期刊评价中的应用[J]. 中国科技期刊研究, 2004, 15(6): 658-660. [本文引用:1]
[11] 凌春艳, 莫琳. 自然科学学术期刊质量指标体系的属性数学综合评价模型[J]. 数学的实践与认识, 2004, 34(5): 1-7. [本文引用:1]
[12] 苏新宁. 构建人文社会科学学术期刊评价体系[J]. 东岳论丛, 2008, 29(1): 35-42. [本文引用:1]
[13] 李修杰, 陈景武. 运用判别分析法建立的期刊评估指标体系[J]. 江西图书馆学刊, 2006, 36(3): 48-50. [本文引用:1]
[14] 俞立平, 潘云涛, 武夷山. 学术期刊评价中主成分分析法应用悖论研究[J]. 情报理论与实践, 2009, 32(9): 84-87. [本文引用:1]
[15] 苏为华. 多指标综合评价理论与方法问题研究[D]. 厦门: 厦门大学, 2000: 151-166. [本文引用:1]
[16] 侯文. 对应用主成分法进行综合评价的探讨[J]. 数理统计与管理, 2006, 25(2): 211-214. [本文引用:1]
[17] Pearson K. On Lines and Planes of Closest Fit to Systems of Points in Space[J]. Philosophical Magazine, 1901, 2(6): 559-572. [本文引用:1] [JCR: 1.596]
[18] Frank C R J. Statistics and Econometrics[M]. New York: Holt, Rinehart and Winston, Inc. , 1971. [本文引用:1]
[19] Gujarati D N. 经济计量学精要[M]. 张涛译. 北京: 机械工业出版社, 2004: 204-205. [本文引用:1]
[20] Hoerl A E, Kennard R W. Ridge Regression: Biased Estimation for Nonorthogonal Problems[J]. Technometrics, 1970, 12(1): 55-67. [本文引用:1] [JCR: 1.424]
[21] 中国科学技术信息研究所. 2008年版中国科技期刊引证报告[M]. 北京: 科学技术文献出版社, 2008. [本文引用:1]