为提高SPARQL语句的查询效率,使用RDF模式信息来精简SPARQL基本图模式,然后使用B树结构快速估计SPARQL连接图的节点大小及边权值,使用连接代价估计并结合动态规划方法找到最优逻辑查询计划,实验对比表明,使用本方法的SPARQL查询效率比Jena要优秀,和Sesame性能相当。
In order to improve SPARQL query efficiency, this paper uses RDF schema to simplify the BGP of SPARQL, and then estimates each node’cardinality and the weight of each edge through B-tree indexes quickly. After that, it uses the methods of joining cost estimation and dynamic programming for the optimal logical query plan. The result of the experiment shows that the new method improves the SPARQL query efficiency,while the performance of this method is as good as Sesame, and much better than Jena.
目前,对RDF文档查询优化研究主要分为两个方面:一种是对RDF文档建立有效的索引机制,如文献[1]和文献[2]对RDF文档的索引机制的研究,以及Oracle、MySQL等关系数据库对RDF文档的序列化索引机制;另一种是对RDF标准查询语言SPARQL的优化。前者主要依赖于RDF的索引结构、磁盘索引存储方式或数据库的特性来达到较高的I/O吞吐性能;后者从分析SPARQL语法语义的角度,研究其查询机制,找到最优的逻辑查询计划。本文的研究属于后者,对于RDF的存储使用B树结构来建立多个策略的索引文档。
对SPARQL优化的研究,杜小勇等[ 3, 4]分别从属性相关性的角度来调整SPARQL语句中连接操作的选择度估值,以及使用自适应存储系统FlexTable来改善查询效率;叶育鑫等[ 5]采用SPARQL语义约简规则以及选择估值策略融合的方法设计SPARQL的优化算法; Stocker等[ 6]提出了一种利用元组模式的选择度估值寻找元组模式最优连接顺序的方案,并已应用于Jena的SPARQL查询优化器ARQ[ 7, 8]中;Vidal等[ 9]提出了一种对SPARQL查询模式进行分组的策略;Huang等[ 10]分别采用贝叶斯网和链直方图的方法进行选择度的估计来优化SPARQL查询;Schmit 等[ 11]在理论上提出了SPARQL的两种类型的查询优化方法:代数优化和语义优化。
本文提出SPARQL在基本图模式下的优化策略,即融合RDF模式信息和连接代价的优化算法,并利用B树
索引RDF数据集,使用LUBM[ 12]基准测试集结合Jena、Sesame框架进行对比实验。
SPARQL类似于SQL查询语言的select-from结构,其执行需要相应的查询处理器对SPARQL语句进行编译。由于SPARQL在编译过程中会进行关系代数等价转换,而关系代数的等价形式可能有多种,各操作子(如连接、投影等)的执行顺序,尤其是连接操作的代价,以及操作子的具体实现方式都有差异,因此就存在对SPARQL的各种逻辑优化策略。SPARQL的基本图模式是所有模式中最基础、使用最多的查询模式,也是当前SPARQL优化的研究热点。基本图模式的优化目的在于确定图模式中三元组模式的执行顺序,以尽量减少连接操作的执行代价。
基本图模式(Basic Graph Patterns,BGP)由三元组模式(Triple Patterns)及其约束构成,在进行图模式匹配时,BGP中的每个三元组都必须进行匹配,结果集是各三元组模式匹配的连接操作得到的结果集。由于SPARQL其他图模式,如可选图模式、并图模式等最终都会进行BGP匹配以及其他代数运算,对BGP的优化更为本质。因此本文主要研究如何通过优化BGP来实现SPARQL的优化。
和其他语言一样,SPARQL有自己的语言规范。SPARQL语法共有5部分构成[ 13]:命名空间(NS)、数据集(RDF Dataset)、查询方式(QF)、图模式(GP)、结果修饰(SM)。表1给出了LUBM基准的第2个查询语句,其中“//”后面的语句是为了便于说明,由笔者加进去的。
| 表1 LUBM基准给出的第2个查询语句Q2 |
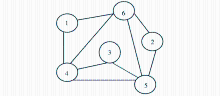
如果将BGP中的每个三元组模式映射为节点v,若三元组模式之间存在公共的变量,则节点之间添加一条边e,这样处理后将得到SPARQL的连接图,该连接图为无向连通图,按照用户输入的图模式中的三元组顺序编号,对于表1中的SPARQL示例,将产生如图1所示的连接图,连接图越复杂,表明三元组之间的关联越多,查询的代价可能越大。
本文提出的优化算法大致分为两个步骤,首先利用RDF的模式信息对SPARQL图模式进行简化处理,然后在此基础上利用连接代价和动态规划方法寻找每一次迭代的最优连接顺序,最终得到其最优查询计划。
文献[5]中提出了两条约简规则可概括为:
(1)对于含有公共变量的图模式{?x rdf:type C1. ?x rdf:type C2.……},其中,C1和C2都是RDF中的概念,C1⊆C2,图模式可简化为{?x rdf:type C1.…… };
(2)对于类似于{?x rdf:type C1. ?x p o.……}的图模式,其中p为非rdf:type类型的属性,可直接简化为{?x p o.……}。
这两条规则都力图保证图模式中的TP的特殊化而非泛化,剔除泛化的TP,可以减少集合操作,缩短查询时间。但这两条规则都存在使用的假设前提,文献[5]中并未提及,对于第(1)条规则,它假设查询引擎具有一定的推理能力:对于某实例来说它是其直接父类的实例,那么它也是其间接父类的实例,但对于不同的查询引擎可能并不支持推理,因此这个图模式匹配的结果可能是空集;对于第(2)条规则,它忽略了三元组模式的定义域或值域的范围,在示例中,当谓词p的定义域是多个概念的集合,那么(?x rdf:type C1)模式具有进一步的约束能力,不应统一处理为该三元组谓词p的定义域为单一概念。
因此,对于上述第(1)条规则,本文假设查询引擎具有推理能力,执行规则(1)进行简化,但要注意的是针对不同的查询引擎,简化与否的执行结果是不同的;对于第(2)条规则需要根据模式信息考察谓词p的定义域或值域是否为单个概念:如果是,则可直接按规则(2)简化,如果不是,那么图模式将不进行简化处理。
另外,RDF中用rdfs:subPropertyof表示属性之间的继承关系,且子属性模式的元组蕴含在父属性元组中,因此对图模式中存在属性间继承关系的一些TP也可进行简化。本文增加第(3)个简化规则:
(3)对于含有公共变量形如{?x p1 ?o. ?y p2 ?o.……}的图模式,其中p1是p2的子属性,可简化为{?x p1 ?o.……},由于该子属性模式的匹配结果集蕴含于父属性模式的匹配结果集,两个结果集进行连接运算的结果集同子属性模式匹配结果集一致。
SPARQL查询效率通常和连接操作的执行方式、连接操作左右数据集的大小、连接产生的中间结果集大小有关。连接执行的方式属于查询的物理执行阶段,连接操作左右数据集的大小将影响操作的迭代及数据访问次数,连接结果集大小将影响下一次的连接操作。 SPARQL图模式连接优化的关键在于找到最优的查询计划,即最优的三元组模式连接顺序。
(1)RDF数据集B树索引及节点大小估计
B树是目前构建数据库索引广泛使用的技术,其查询效率等价于二分查找。本文使用AlleGroGraph[ 14]平台来构建RDF文档的B树索引,AlleGroGraph以5元组的形式存储RDF陈述(Statement),即spogi,分别对应三元组陈述的主语、谓语、宾语和具名图、元组ID。由于三元组模式的变量位置只有主语、谓语、宾语三个地方,那么三元组的模式将会有8种情况。去掉最特化的模式(s p o)和最泛化的模式(?s ?p ?o),将得到6种三元组模式:(?s p o)、(?s ?p o)、(s ?p o)、(s ?p ?o)、(s p ?o)、(?s p ?o)。为了节省存储空间,本文只选择了spogi、posgi、ospgi这三种索引策略,可覆盖上面6种模式。
对三元组模式匹配结果大小的估计是建立在B树的基础上,比如三元组模式(?s p o ),假设主语变量?s的Hash值的取值范围设置为[0-0xff],那么可以确定整个三元组的Hash值的取值范围,假设为[n1,n2],对于该取值范围在B树上查询计算键值在n1和n2之间的结果数N,这两个结果之间的数据包含了整个三元组模式匹配的结果。对于该结果基数的估计cart(t),本文提出如下公式来计算:
cart(t)=3×N/4 (1)
由于B树节点键值数目在[m/2,m-1]之间,故乘以3/4表示对B树利用率的估计。
(2)边的权值估计
本文对边的权值使用对节点词的连接操作的结果集大小的估计来计算。对于连接操作结果集大小的估计使用了对节点基数的估计值,并采用了一些启发式规则。本文提出如下公式来估计连接操作结果集的基数:
T(R 
其中,R和S分别表示三元组模式匹配后的结果集,T(R 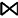
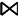
①当左右操作数没有公共变量时,连接图中子图之间没有直接的边连接,这种情况泛化为笛卡尔积,即R×S,这时s=1,那么:
T(R 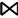
②当左右操作数有公共变量时,假设公共变量的集合为VRS=VR∩VS,W(R, VRS)表示R操作数上的VRS变量集上的不同值的数量,W(S, VRS)表示S操作数上的VRS变量集上的不同值的数量,并假设不同值在操作数上都是均匀分布的。当W(R, VRS)≤W(S, VRS),假设操作数R在变量VRS的值都在S上,那么R中每个元组在S中有 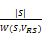
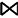
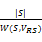
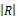
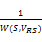
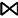
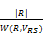
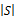
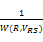
T(R
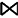 | (2) |
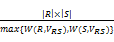
其中,对W(R,VRS),W(S,VRS)的估计,本文再次利用节点基数的估计值和相关统计信息来计算。
表2给出了本文对三元组模式中变量的不同值的数量的估计。这里只考虑了谓语位置为常量的模式,谓语为变量的情形在实际使用过程中很少会用到。
| 表2 三元组模式匹配结果中变量的不同值估计 |
表2中对于t3模式中?o的不同值数估计有些特别,原因在于?o的不同值数根据RDF数据集结构、大小的不同而可能有很大的差异,因此如果依赖card(t3)对其产生固定的估值将造成估值不准确的结果。对此,本文使用B树索引统计了在所有指定属性下该模式中变量?o的不同值数,记为dintinct(?o)并生成属性值表。得到估值后,就可以按公式(2)进行中间结果基数的估计。
(3)基于连接代价的动态规划算法
本文使用动态规划方法在整个连接图空间中查找最优的执行顺序。动态规划的核心思想在于将多阶段问题转换为一系列单阶段问题,下一阶段求解时利用上一阶段的结果,避免了重复计算,提高了求解效率。对于本文连接图最优执行顺序求解的每一个阶段需要求解的项目包括:连接操作结果集大小的估计T、连接操作最小代价的估计C(使用中间结果集基数的和来估计)、该阶段最佳执行顺序Q。最小代价对应最佳执行顺序。该算法的具体执行过程如下:
Input:初始化的连接图
Output:连接图的最佳连接顺序
执行阶段:1.计算每一条边T,C,Q
2.计算每两条连接边的T、C、Q,可利用阶段1的结果
3.计算每三条连接边的T、C、Q,可利用阶段2的结果
4.直至所有连接边都计算完成,输出该阶段的Q
对于图1中的连接图,首先初始化图中的节点大小及边的权值,第1阶段的估计值如表3所示:
| 表3 第1阶段求解结果 |
其中,E(eij)表示边的权值,使用公式(2)计算。第1阶段的T为初始化图中边的权值,由于第1阶段之前没有中间结果产生,因此最小代价C的估计都为0,Q的估计则根据启发式规则将cart(vi)最小的排在前面。表4给出了第2阶段的估值情况,对于Q则根据最小C值对应的左深连接树(Left Deep Join Tree)来确定,利用右集合的索引进行快速连接,减少内存使用率,避免中间关系的重复构建。
| 表4 第2阶段部分求解结果 |
对于第3阶段的求解过程和上述阶段一样,不再冗述,这样直至所有的边都进行了代价估值,算法将在最后一个阶段输出最小代价对应的连接顺序,即最优查询计划。基于代价的动态规划优化算法在连接图全局中搜索最优的执行顺序,中间阶段的最优执行顺序可能在下一阶段变得不是最优,这样保证了最终结果的全局最优性。
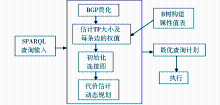
本文整个算法的执行流程如图2所示:
算法首先对用户输入的SPARQL语句利用模式信息进行简化,接着利用B树索引结构以及事先统计出的属性值表对元组模式进行基数估计,确定边的权值,初始化连接图,之后使用基于连接代价的动态规划方法结合左深连接树得到最优的逻辑执行顺序输出。
该算法先检测BGP是否符合上述第(3)条简化规则,对检测出符合规则的模式,在BGP中删除,简化后再进行规则(1)和规则(2)的检测与简化。模式信息简化BGP算法描述如下:
Input: 初始BGP
Output:简化的BGP
初始变量:含谓词type的三元组模式集合typeSet、谓词为常量的三元组模式集合pSet
FOR each tp in BGP
将满足条件的tp分别放入typeSet和pSet中
FOR each tp in pSet //先进行规则(3)的检测
IF 符合规则(3)对模式的要求
IF tpi.p subPropertyOf tpj.p
pSet.remove(tpj) BGP.remove(tpj)
ELSE IF tpj.p subPropertyOf tpi.p
pSet.remove(tpi) BGP.remove(tpi)
FOR each tp in typeSet //执行规则(1)和规则(2)的检测
IF符合规则(1)对模式的要求
IF tpi.o subClassOf tpj.o
typeset.remove(tpj) BGP.remove(tpj)
IF tpi中的变量在pSet中有对应的三元组,且符合规则(2)对模式的要求
typeset.remove(tpi) BGP.remove(tpi)
ELSE IF tpj.o subClassOf tpi.o
typeset.remove(tpi) BGP.remove(tpi)
IF tpj中的变量在pSet中有对应的三元组,且符合规则(2)对模式的要求
typeset.remove(tpj) BGP.remove(tpj)
该部分实现依赖于AlleGroGraph平台的B树索引结构,如对于数据集构建的索引树节点允许的子节点数为124,那么每个节点可拥有的键值数为123个,每个指向子节点的指针被顺序赋予0-123索引号。对于每个节点,先计算其Hash(v)值的范围[h1,h2],再到B树上计算N=count(h1≤h≤h2),利用公式(1)得到节点的基数估计cart(v)。基于连接代价动态规划算法的每一个阶段都利用上一个阶段的执行结果,其中涉及到求子图的算法,其基本思想是在上一阶段子图集合上分别添加一条边得到。算法描述如下:
Input:简化的连接图G
Output:最优执行顺序Q
初始变量:第1阶段连接子图为连接图的边,第1阶段的连接操作最小代价的估计C=0;假设变量subG用于保存上一阶段的子图集合;V表示初始连接图节点集合;E表示初始连接图边的集合;
FOR each v in V
使用公式(1)计算cart(v)
FOR each e in E
使用公式(2)计算每条边的权值
FOR i from 1 TO numv-1 //numv表示连接图的节点数目
//subGraph(i,g)表示在连接图g中选取包含i+1个节点的联通子图的全部集合
FOR each gi in subGraph(i,G)
根据公式(2)计算e的结果集大小,得到T(gi)值;
在上一阶段subG中得到与gi匹配的子图集合,
并计算各子图的T+C值,取最小值作为C(gi);
保存T(gi)和C(gi),以及最优顺序,供下一阶段调用
输出迭代最后的执行顺序Q
subGraph(i,g)算法:i>=1
//假设vset表示最终得到的集合变量
FOR each element in subG
E1={E-element.e} //G中剔除element图中的边得到的集合
FOR each vj in element.v //遍历子图中每个节点
IF E1.getedge(vj)!=null //如果E1中存在与子图中节点vj相连的边
vset.add(element, E1.getedge(vj));//在该子图基础上将该边加入
输出vset
整个优化算法是在用户输入时动态计算,由于BGP的规模一般都在10-15个TP左右,更复杂的查询很少见,所以利用模式信息简化查询基本不用耗费时间。基于连接代价的动态规划方法利用了B树的索引结构,可以快速估计出相关值,由于图模式相对于三元组实例的规模要小很多,其计算时间可以忽略不计。
本文的实验将从算法在不同规模的BGP、不同大小数据集、不同查询引擎三个方面的执行情况进行考察。
本文使用的实验平台是Intel(R) Core(TM) i7-2630QM CPU @2.00GHz,内存3 058MB RAM,开发环境为Java。使用的数据集来自LUBM(LeHigh University Banchmark)[ 12] , LUBM是测试SPARQL性能的基准,提供了14个SPARQL查询语句以及相应的大学本体元数据Univ-Bench,对于测试数据集,LUBM提供数据产生器用于产生基于Univ-Bench的测试数据。本文使用UBA产生5个不同大小的数据集,其三元组数、实例个数、占用空间(MB)分别为Lubm1 (82415,20659,8)、Lubm2 (516116,129533,50)、Lubm3 (1052895, 263427,102)、Lubm4 (1616472, 404743,158)、Lubm5(2224750, 556572,218)。由于14个查询语句有若干是偏重于测试查询引擎的推理功能,即发现数据集中隐含的信息,因此本文对这些语句进行了相应的修改,增加了常见的串型和星型模式,最终确定了10个不同规模的查询语句,其特征如表5所示:
| 表5 本文使用的查询语句的特征 |
(1)不同查询语句优化性能的比较
首先选择在Lubm3数据集上进行10个查询语句的优化测试,每个语句连续执行10次后取平均值,结果如表6所示:
| 表6 在Lubm3数据集上的优化测试结果 |
其中,第2行表示在优化前各个语句上的执行时间,可以看到查询语句的规模影响查询的速度,但并不表示查询语句规模越大执行时间越长,相同规模的查询语句的执行时间也可能产生很大的差异,如Q2和Q3以及Q7和Q8,这主要是由于查询语句的连接图不同,执行过程中中间结果集大小不同导致连接操作的代价不同而导致的。
第3行表示利用本文的优化算法找到最优逻辑查询计划所耗费的时间,总体上来看,算法寻找最优执行计划的时间相对于整个执行过程来说所占的比例较小。同时也注意到,最优查询计划的搜寻时间的长短和查询语句的规模大小也不一定成正比,如Q4和Q7。搜寻时间与查询语句的结构(有无可简化的元组模式)以及连接图的复杂度有关。
第4行是执行优化查询所消耗的时间,第5行是寻找最优计划的时间与查询执行时间之和。总体上看,本文的算法比优化前的执行效率要高,有些语句的执行时间要比优化前小很多,如Q1、Q2、Q4等。对来自LUBM 中的Q1语句,采用本文的算法进行简化,大大缩短了查询时间;对于Q2,其连接图见图1,结构相对来说比较复杂,经过本文算法的优化,调整其连接顺序,执行的效率也提高很多;对于查询语句Q5和Q6,执行优化后的差异不大,是由于原始语句已经是较优的执行顺序,算法优化的空间不多造成的。
(2)不同数据集与不同查询引擎的优化性能对比
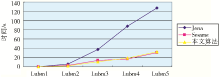
本文选择中等规模的Q2语句作为优化对象,分别在5个数据集上进行实验,并和常见的查询引擎Jena和Sesame的查询性能做对比,结果如图3所示:
可见,Jena的查询性能随着数据集的增大,其性能严重降低,这主要是由于Jena的查询优化算法更适合BGP模式比较简单的情况,对于复杂的图模式,它需要更好地估计三元组模式的选择度,选择度估计的好坏直接影响其优化算法的执行性能。而本文的方法和Sesame的性能相当,Sesame采用对未绑定变量个数的估计来确定查询执行的代价,未加入执行计划的模式中的未绑定变量越多执行,代价越高,未绑定变量在其他模式中出现次数越多,代价越低,这种启发式方法一般情况下能够找到最优的查询计划,但可能因忽略模式间的数据关联而陷入局部最优。
同时,对于较小的数据集如Lubm1、Lubm2优化性能并不明显,而对于较大的数据集,优化性能则非常显著。这是因为:较小数据集的中间结果集的本来就相对较小,经优化后的查询代价和未优化的查询代价差距不太大,优化的效果不明显;而对于较大的数据集其中间结果集较大,经优化执行的中间集会显著减少,连接代价会明显降低,优化的效果就比较明显。
本文设计并实现了结合语义简化及连接代价模型的SPARQL查询优化算法,该算法除只需要增加一个属性值表的统计预处理过程外,不需要其他任何的数据准备,结合B树索引获取估计参数,构建代价模型,采用左深连接树和动态规划方法查找最优计划,在大数据集上测试表明该优化算法比Jena查询引擎的执行效率要优,和Sesame的查询性能相当。
本文只探讨了SPARQL在BGP模式下的优化情况,虽然其他图模式最终都会转换为BGP的代数运算,但在执行过程中仍可采取不同的优化策略,同时除了从逻辑层面考虑优化效率外,可引进多线程或使用多CPU进行多个图模式匹配,设计分布式查询引擎,使用并行查询优化技术(Parallel Query Option,PQO)进行优化。另外,除了上述方法外,一个重要的方向及当前研究热点是从RDF的索引存储角度考虑,设计有效的索引机制,以处理海量语义数据。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|