在BA无标度网络中引入社会福利博弈模型,建立动态舆论演化博弈模型,研究传播率对舆论演化的影响,并仿真上述博弈模型,探讨政府进入舆情传播的时机的优劣。结果表明,政府介入舆情传播并不是越早越好,因为传播比例、政府介入的时机会共同作用影响舆情的传播趋势;并且小世界性更利于信息的共享而使舆情传播的态势趋于平稳和明朗,这值得政府加以利用。
This paper introduces the traditional social-welfare game model into the BA scale-free network to find out the relationship between the model and the evolutionary process of the public opinion. Taking into account of the study and imitative behaviors to the other gamers in the information structure, it carries on the simulation experiment, and gets the conclusion that small-world effects have positive impact on the information communication and gambling result, so it is a useful tool for government, while propagation speed and the opportunity when the government should control the public opinion are cooperated to influence the information dissemination. In a word, it is not that the earlier the government steps in, the better result we can see.
自1994年4月中国正式接入国际互联网以来,网络已经成为大众生活不可或缺的一部分。2011年7月19日,中国互联网络信息中心(CNNIC)发布《第28次中国互联网络发展状况统计报告》,截至2011年6月底,中国共有网民4.85亿(较2010年底新增网民2 770万)[ 1]。
互联网已渗透到了社会生活的各个方面,甚至改变了我国社会舆论的生态环境,形成了崭新的网络舆论场所。人们网络行为的增多,使得虚拟网络世界中的网络行为与现实世界中的行为已经不分彼此,共同构成了信息传播的动力和源泉。社会网络化程度的加深使得对舆情的研究已经不能避开网络的因素,因此对网络舆情的研究得到了越来越多的重视。
研究者不断探究网络舆情的演化机制,希望能够用科学的方法来“计算网络舆情”,从海量的网络信息中发现舆论情势和变化规律,使看似错综复杂的网络舆情,尤其是负面网络舆情能够在科学的测量方法和有效的学术解读下,变得清晰,进而对其进行有效的预警和疏导。
国内外学者对舆论的演进采取了不同的方法进行研究。Hegselmann等[ 2]从现实社会中人们之间相互影响的实际情况出发,提出了“有限信任”模型,并对其进行了仿真研究。Weisbush[ 3]和Lorenz[ 4]对“有限信任”的框架继续推进了一步,采用信任阈值来限制个体间的交互,较为真实地反映了现实社会中的交互情况。诸多学者用经典传染病模型,如SIR模型[ 5]和SIS模型[ 6]来研究完全联通的社会接触网络上的传播行为。另外,学者还尤其针对谣言的传播进行了研究。Sudbury[ 7]最早借鉴流行病SIR模型研究谣言的传播,在随机网络上研究了该模型,发现谣言的传播人数会有上限。Zhou等[ 8]则证明了在常见的一般网络中(包括无标度网络、有群落结构的网络和小世界网络等),随机网络是最易传播谣言的。王根生等[ 9]构建了元胞自动机演化模型,仿真结果表明能够较好地拟合舆情演化规律。韩少春等[ 10]建立了动态舆论演化博弈模型,研究了羊群效应在舆论演化过程中的产生机理及其动态发展。也有学者通过直接研究某个网站的各项数据来达到研究传播行为的目的,比如,Golder等[ 11]研究了在线交友网络Facebook,通过对420万用户的研究发现,用户的好友平均数是180,中值是144。刘志明等[ 12]通过对3起突发事件微博数据的实证研究,构建了对意见领袖特征进行分析的理论框架。
笔者从韩少春等[ 10]的动态舆论演化博弈模型中发现博弈模型可以很好地诠释网络舆情传播中个体行为的变化,社会福利博弈模型中博弈双方的分类意义又恰好可以描述网络舆情中政府与网民之间监管与被监管的状态,所以本文将社会福利博弈模型引入BA无标度网络中,在个体行为决策变化的基础上研究了网络舆情这个作为个体的集合的演变过程。
对于任何一个博弈模型,可以证明必定至少存在一个纯策略或混合策略的纳什均衡。本文构造的博弈模型中,博弈双方即为互联网环境下的参与者,按其职能分为两类:网络舆情监管部门以及舆情参与讨论传播者,也就是政府和网民。对于一则负面消息的网上传播,政府有两种状态:一种是没有发现舆情,所以不采取任何治理措施;另一种是发现舆情后及时遏制传播势头以减小负面影响带来的社会损失,方法包括线下解决舆情关注的社会问题,线上查处散播谣言的网民以正视听。而对于网民来说也有可能因为上网习惯处于两种状态:一种是因为从众心理而选择传播这则负面消息;另外一种是作为理性人希望得到更多的消息来明辨是非,亦或是因为不关心而选择暂不进行传播。如上所述,引入博弈模型可以更好地从个体角度出发观察群体中的舆情演化机制。
网络社区中,如果网民个体都倾向于传播一则负面信息时,政府的网络监管部门就需要进行监管并查处消息传播者,这样才能有效控制由于消息传播而可能引起的社会恐慌;相反,如果网民个体大多数很理性,对负面信息能够做到不信不传,那么网络监管部门就没必要进行监管,因为此时监管的成本大于带来的社会收益,相当于浪费社会资源。这与社会福利博弈模型中政府与流浪汉之间的博弈情况极为相似。所以本文试图用社会福利博弈模型描述网络中网络监管部门与网民之间的博弈过程,找到网络中消息传播的某些规律。
对于网络上一则负面消息的传播,本文设政府因为没有发现舆情而选择不采取任何措施监管网络的概率是α,政府发现舆情选择监管网络并查处散播消息的个体的概率为1-α;网民个体则以概率β选择不传播消息,以1-β的概率选择传播消息。
那么,双方不同的策略组合收益如表1所示:
| 表1 博弈模型的收益矩阵 |
求解此博弈模型的均衡策略,本文得到如下一些结论:
(1)当网络中的个体传播消息的概率β*>0.2时,政府网络监管部门一定会选择监管并查处来净化网络,安稳社会。β*是本文模拟仿真中所用到的传播率,其含义是一则消息每个单位时间内的传播人数较之前一小时传播人数增加的比例。
(2)当政府部门监管查处网络不实消息的概率α*>0.5时,网民会选择不传播的策略来应对。
根据结论(1)中所得,当传播率大于0.2时政府一定选择监管网络这个策略。但是实际情况中,并不能确定传播率0.2是政府开始监管的最佳时间点,所以笔者对上述的收益矩阵进行了变换,希望传播率β*可以变成一个可控变量,这样可以通过β*的变化对政府收益的影响,寻找政府进入舆情控制的最佳时间段。
改变后的收益矩阵如表2所示:
| 表2 含有变量的博弈模型的收益矩阵 |
C表示政府监管网络所需花费的成本,本文设C=1。M表示监管行为所能带来的社会收益,反之-M则代表监管不当带来的社会损失。很明显对于一则负面消息的传播,当网民倾向于进行传播时,政府监管查处传播者的行为能适当消除事件的负面影响,减少社会损失;另一种情况下,当网民都不选择传播行为时,政府的监管行为也不会有社会收益或损失。
求解此博弈模型得到其均衡策略为:β*=1/2M。找到传播率β*与社会收益M之间的关系,模拟仿真中将用到这对关系,通过调整β*来改变M值以观察政府收益的变化。
前人的研究工作大多是探究能够更好拟合实际数据的模型,模拟的过程首先是假设模型符合实际情况,在此基础上改变模型中的可变参数,然后分别与实际数据拟合以证明模型的拟合性,最后再重新研讨不同参数下模型的优劣。
本文的优点在于先发掘了模型中的可变参数与实际传播过程的联系,即社会福利博弈模型的最优解H就是本文模拟仿真中所用到的传播率,它与社会收益存在函数关系;这已经说明模型是符合实际情况的,两者有密切联系,不需要数据拟合这一步骤,可以直接探讨不同参数下模型的优劣,即不同参数下实际情况的变化。
将互联网的社区网络看成是一个BA无标度网络,假设模型中网民共有N人,所有网民拥有相同的策略集与收益矩阵。由于信息的不对称,网民个体无法确定政府的策略选择。所以假设初始网络中的网民节点,因为无法得知政府的决策,会凭自己的传播习惯先行选择各自的传播策略,这与真实网络中一条信息开始被传播时,网民会依据自己的信息传播习惯自由选择传播行为的事实是相符的。
本文模型的交互规则中假设网民策略的选择会影响到政府的应对策略,社会福利博弈模型的引入本身又说明政府策略的调整会影响网民策略的选择。但是真实情况是:对于网络上传播谣言的人的处罚案例非常少,政府的网络监管似乎对网民没有很大的威慑性,这是因为我国的网络立法并不健全,网络技术也还不够完善。本文的模型假设是:网民是否传播一条消息的行为由自己的上网习惯决定,受事态的发展和其他网民的态度影响,也会根据政府的监管调整自己的决策行为。
首先构建一个BA无标度的初始网络,网络中的每一个节点看作是真实网络中的网民个体。随后引入改变后的社会福利博弈模型。
每一轮博弈开始时网络中会加入一个新节点s。在每j轮的博弈中,新加入的网民节点s可以获得自己i个邻居节点的决策行为,并选择这i个邻居节点中大多数人选择的策略作为第j轮中自己的决策,真实社会中可以用从众行为来解释。其中,与新加入的网民节点s相连的所有节点中第i个节点的收益用Pi,j表示,第i个节点选择的策略用di,j表示,di,j取值为0或1,其中1表示传播,0表示不传播。
因此在第j轮博弈中,网络中新加入的节点s选择的策略应为:
[C,I] = max [number(dx,j=0),number(dx,j=1)]
ds,j=I (1)
新节点s选定策略后,政府计算第j轮的政府总收益Pj应为:
Pj=∑ Ps (s=1,2,…,j) (2)
此外,第j轮博弈结束的时候可以得到一个实际传播率L,其含义是第j轮博弈结束时选择传播策略的人数较之第j-1轮中选择传播的人数增加的比例。与此同时给定一个政府监管传播率H,即假设政府能够容忍的最大传播率,H是变量,可以改变。如果实际传播率L小于H,政府就选择不监管网络的策略;而一旦L超出了H的范围,政府会发现舆情并开始监管网络。用dg表示政府决策,其值为0或1,其中0表示不监管,1表示监管并查处散播消息者,所以可以定义第j轮的交互规则如下:
if L<=H;
dg=0;(3)
else dg=1;
政府策略选定后,新加入的节点与其邻居节点会根据社会福利博弈模型的收益矩阵改变自己的策略,以使收益最大化。
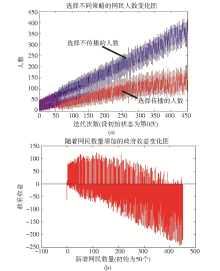
本文使用Matlab语言,先定义初始节点m0=50,每次新加入的节点的度m和网络总规模N=500构建BA无标度网络,而后引入社会福利博弈进行仿真,结果如图1所示:
从图1(a)中可以看到,当政府对于传播率的控制阈值控制在0.2时,政府介入舆情传播控制的时间很早,能够有效控制舆情传播人数。刚开始的一段博弈中,网民选择何种策略多是由各自的上网习惯决定,受邻居影响不大,所以选择两种策略的人数随着知道消息的网民人数的增大而交错上升。因为政府介入舆情传播控制的时间很早,所以随着时间的推移,网络中的新加入的网民个体及其邻居能够较快发现选择不传播消息会获得较大的收益,表现在选择不传播策略以应对政府监管行为的人数增长较快。本文中的政府决策随着传播率的变化而时时改变,并不是根据网民节点策略进行调整,从图1(b)中也可以看出,政府收益并不稳定,会因为网络中网民节点策略的调整或正或负。仅从政府收益的正半轴看,开始时政府的收益有逐渐增大的趋势,随着网民人数的增加反而开始下降,直到最后一直保持负数状态,不再有收益。对政府而言,这说明早期介入一则消息的舆情传播控制,能够有效地控制社会舆论,为政府带来收益。但是在传播的后期,即使选择传播的人数变少,基数整体的扩张依然会使实际传播率大于阈值且居高不下,政府势必需要一直采取监管策略,而越到后期网民越表现为选择不传播策略的人数增长较快,这两种情况一起出现导致的结果就是政府收益持续为负。
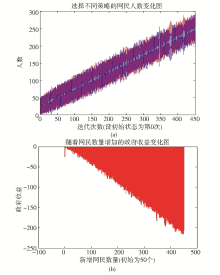
适当增大政府的传播率控制的阈值,H=0.5的情况如图2所示:
可以看出,图2(a)中政府介入舆情控制的时间点有所推迟,但传播人数并没有出现失控的现象,选择两种策略的人数依然交替上升。虽然政府的收益状况始终为负,但从图2(b)中可以看到政府收益是在平稳下降,尤其值得注意的是图2(b)到了舆情传播后期政府收益与图1(b)相比较反而损失比较小。这是因为图1(b)中的后期选择不传播策略的网民占大多数,可是阈值控制过小导致后期政府可能要一直采取监管措施,那么政府的收益势必显著下降且速度较快。而图2(b)中尽管后期基数整体的扩张也必然导致政府一直处于监管状态,可是因为也有相当多的网民选择传播策略,所以此时政府的监管反而更有意义,而不是在浪费资源去监管本不需要控制的舆情。
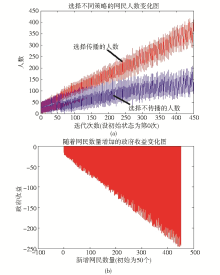
再次增大H的值,当设定H=0.8时,结果如图3所示:
可以发现,图3(a)中政府采取措施的时间太晚,舆情已经传播开来,有无法遏制的势头。图3(b)中的后期收益有波动,不像前期一样稳定,这是因为后期政府虽然一定采取监管措施,但只对采取措施后的新加入节点和其邻居节点有制约作用,所以表现为这种补救可以挽回一些损失,却也失去了控制舆情传播的机会。
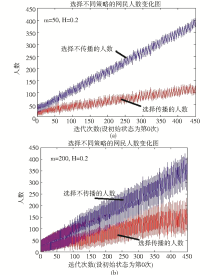
不同m值对选择不同策略的人数变化的影响如图4所示:
可以看出,当H值不变时,m值越大,人数增加时的波动性就越大,这是因为小世界性可以促使最优策略的快速扩散,使得节点容易形成一致意见。对于每一轮的策略演化,都会产生一定量的最优策略节点,但由于存在随机性,优势策略带来的收益会产生偏差,造成短期内非最优状态。m值越大,对于每一轮博弈加入网络中的新节点来说,其邻居节点的意见越呈现出多样性,所以新节点策略的选择越发不稳定,在图4中表现为曲线的波动性大。
本文在BA无标度网络中引入社会福利博弈模型,通过仿真模拟网络中各节点的行为选择,研究了舆情的演化过程。通过对比仿真实验结果发现,对于一则消息的传播,政府介入舆情监管并不是越早越好,过早介入虽然可以起到控制舆情发展的作用,却也带来不必要的资源浪费。从网民策略更新的结果中也可以发现,小世界性将会利于信息的共享而使策略的更新趋于平稳。对于不同性质事件的舆情控制,确定不同的合理的控制点来实现社会舆论的稳定,将是下一步的研究重点。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|