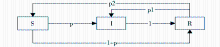互联网是一种连接度分布函数具有幂律形式的复杂网络,且网络节点的连接度没有明显的特征长度,具有无标度性。为了解释幂律分布的产生机理,Barabási等^{[ 14]}提出一个无标度网络模型,被称为BA模型。该模型考虑到实际网络具有两个重要特性:增长特性,网络的规模是不断扩大的;优先连接特性,新节点更倾向于与那些具有更高连接度的“大”节点相连接。基于网络的增长和优先连接特性,BA无标度网络模型的构造算法如下:

(1)增长:从一个具有m₀个节点的网络开始,每次引入一个新的节点,并且连接到m个已存在的节点上,这里m≤m₀。

(2)择优连接:一个新节点与一个已存在的节点i相连接的概率∏_i与节点i的度k_i、节点j的度k_j之间满足的关系是:∏_i= 。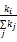

经过t时间间隔后,该算法程序产生一个具有N=t+m₀个节点、mt条边的BA网络。

在SIRS传播模型中,系统中的个体被划分为三类,即易感状态(S)、感染状态(I)、免疫状态(R)。在演化过程中,易感状态个体被感染,感染状态的个体获得免疫能力,而处于免疫状态的个体在获得免疫的同时以概率或者其他作用结果失去免疫力,从而变为易感状态。SIRS模型的状态转移过程如图1所示:

图1

	Figure Option ViewDownloadNew Window
	图1 传统SIRS模型

在微博网络中,用户拥有“关注者”与“被关注者”两种角色,用户B关注用户A,说明用户A是“被关注者”,用户B是“关注者”。当A发布信息时,该信息由A传播给B;当B发布信息时,该信息不会传播给A。因此,用户关注关系指明了信息的传播方向,基于用户关注关系形成的网络应是一个有向网络。微博用户的关注关系如图2所示:

图2

	Figure Option ViewDownloadNew Window
	图2 微博用户的关注关系

以传统BA网络模型构建为基础,统计网络中各节点的入度与出度,每次新加入的节点,根据已有节点的入度进行择优连接,从而建立有向无标度网络。

该模型有三个基本假设:

(1)网络中的用户无新增或移除情况,即模型所构建网络为静态网络;

(2)在微博中,某个舆情所产生的衍生话题数不可估量,假设如果个体对舆情感兴趣,则在演化过程中该个体会重复传播该事件的相关话题;

(3)某用户发表关于舆情的微博信息后,其关注者均能获知该信息。

基于关注关系所形成的微博网络是一个有向的、服从幂律分布的复杂网络,网络中的个体根据是否传播舆情某话题信息分为三种状态:未接收到舆情某话题信息(S)、接收到某话题信息并进行传播或者制造新话题(I)、接收到某话题信息对该信息不感兴趣(R)。三者之间的转移过程如图3所示:

图3

	Figure Option ViewDownloadNew Window
	图3 微博网络中舆情传播状态转移过程

可以看出,微博网络中某个体发布舆情信息后,其邻居个体均接收到此信息,并以p概率由S态转化为I态,以1-p概率转化为R态;当该个体的所有邻居节点均被传播或者该个体为叶子节点,则以1概率转变为R态;而处于R态的个体将以概率p1转变为I态,成为衍生话题的传播者;或者以p2概率转变为S态,成为衍生话题的接收者。其中p1=(λ-q)+q^{[ 13]},r_time为截止t时刻用户收到的关于舆情的信息次数,λ为个体对所接收到的话题不感兴趣但产生新话题的概率,q为衍生话题产生的最大概率,b体现了社会作用程度,b越大,社会作用越大,且p1+p2<1。

刘志明等^{[ 6]}使用真实数据对微博网络结构进行分析,说明微博网络结构与BA网络结构性质相符,均具有幂律分布的特性,所以本文使用模拟数据构建模型的初始BA网络。

以微博网络的用户为节点,以用户之间的关注关系为边,构建符合微博关注网络结构的有向无标度网络。以m₀=3,m=2,N=1 000构建网络,部分节点的入度与出度情况如表1所示:

表1

表1

表1 部分节点度分布情况以及网络平均度(N=1 000) 节点 1 2 3 4 5 6 7 8 9 10 … 平均度 出度 2 0 1 2 2 1 2 2 2 2 … 1.9860 入度 12 2 7 12 14 5 10 9 9 14 … 1.9860

表1 部分节点度分布情况以及网络平均度(N=1 000)

由表1可知,各节点的入度不等于出度,说明所构建的网络不是无向的而是平均度≈2的有向网络。为了验证网络结构的幂律性,其入度分布如图4所示:

图4

	Figure Option ViewDownloadNew Window
	图4 有向无标度网络入度分布

可见,网络中节点的入度分布具有幂律特性,大部分节点的入度较小,即微博网络中的草根节点;而少部分的节点拥有较大的入度,即网络中的名微博用户,模型所构建网络结构符合现实情况。在此网络结构的基础上,根据上述状态转移规则构建舆情传播模型,并进行相关因素分析。

没有衍生话题产生的情况,即参数p1=0,当t时刻个体对前一舆情话题处于免疫状态时,则t+1时刻该个体以p2概率变为对新话题感兴趣的易感态;有话题产生(p1≠0)的情况,设置其余参数p=0.3,p2=0.2。实验结果如图5所示:

图5

	Figure Option ViewDownloadNew Window
	图5 衍生话题是否产生对传播过程的影响

相对于未发生衍生的情况而言,话题发生衍生时系统达到稳定状态所需的时间更长,且稳定时R的比值受到影响。这表现在现实微博网络中是合理的,一个舆情事件一旦产生衍生话题,则该事件的传播时间更长,同时也影响网络中接收到该舆情信息的用户数。

为了研究衍生话题产生的情况下系统的传播规律,实验分析了模型中各参数对传播过程的影响。

由上述传播状态转移规则可知,传播率p、社会影响程度b以及免疫退化概率p2间接影响舆情衍生话题的产生情况。为了阐明随着时间变化,各因素对舆情传播演化过程的影响程度,本文使用定量分析方法进行实验分析,结果如图6所示:

图6

	Figure Option ViewDownloadNew Window
	图6 p、b、p2对传播过程的影响

以p=0.3,b=0.2,p2=0.2为基准,当p增大为0.6时,与传播个体相连的易感个体变为传播态的概率增加,网络中传播者增加,系统稳定时,网络中获知该舆情的个体增多,但是由于话题制造者未发生改变,所以传播的趋势未发生变化,系统到达稳定状态的时间不受影响;当b增大为1,即社会影响度增加,则网络中话题的制造者增多,传播速度加快,舆情较快到达稳定,稳定时接收到舆情信息的个体数增加幅度较大;由于q决定p1的最大取值,实验中设置q+p2=1,当p2增大为0.5时,p1变小,即个体第一次接收到舆情信息便产生衍生话题的概率变小,系统较快达到稳定状态,且稳定时R值减小。这是因为网络中更多的个体变为话题的接收者而非制造者,舆情传播时间变短,传播范围变小;但是当p2<1-q时,p2并不影响最终到达稳定状态的R值。

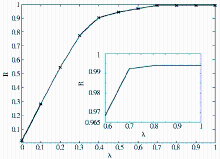
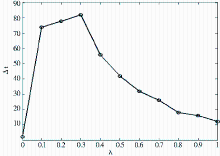
由模型可知,λ表示个体第一次接收到舆情信息则制造衍生话题的概率,λ 值越大,系统所产生的衍生话题越快而且越多,系统越难以稳定。为了考察λ对传播过程的影响,实验分析了λ对系统稳定状态下R值以及对系统弛豫时间的影响。设置p=0.4,q=0.8,b=0.8,p2=0.2,λ 为从0到1、以0.1为间距的取值,每次传播演化100时步,传播100次取其平均值,实验结果如图7和图8所示:

图7

	Figure Option ViewDownloadNew Window
	图7 λ对稳定状态的影响

图8

	Figure Option ViewDownloadNew Window
	图8 λ对系统驰豫时间的影响

由图7可知,随着λ的增大,系统稳定时网络中R值逐渐增大,且在 λ=0.8时,演化达到饱和状态,稳定值不发生变化。结合图8,系统驰豫时间在λ=0.3时达到最大值,而当 λ>0.3时,网络中稳定状态的R值增大但驰豫时间变小,即网络传播速度加快,这与图6中当社会影响增大时,网络传播速度加快具有同样的影响机制。在现实微博网络中,一个舆情事件所产生的衍生话题越多,舆情发展拥有的激活节点数越多,传播范围扩大,从而网络中接收到舆情信息的用户越多,以致影响网络最终稳定状态的R值;但是当网络中大部分节点均为话题制造者时,网络演化到达稳定状态的时间变小,传播速度变快,由以上分析可知,本文所构建的模型符合现实情况。