机械设计是根据人们的使用要求对机械的物理原理、运动方式、能量传递方式、零件的材料和形状大小等进行构思并分析和计算, 将其转化为具体的描述以作为制造依据的过程。机械设计图像是机械设计者在表达其设计以及制造信息时一个十分重要的载体。机械设计者在进行新产品的设计时, 大部分时间是用于对已有的机械设计图像进行查阅, 从中学习经验、获取灵感。传统的机械设计图像检索依赖基于文本的方式[1]:这种检索方式存在两个比较明显的缺点:
(1)检索过程涉及对图像的标注如关键字提取、语义归纳等, 需要人工参与, 随着机械设计图像的不断累积, 这种耗时耗力的方式已经无法满足需求;
(2)标注难以完全描述机械设计图像中的所有信息。
基于内容的图像检索, 主要是利用颜色、纹理、形状及区域等视觉特征对图像进行描述, 并根据对应特征计算相似性完成图像的检索。通过基于内容图像检索得到的结果通常比较客观而且全面, 整个过程几乎不需要人工的介入, 因此将基于内容图像检索的理论和方法应用于机械设计图像检索, 能有效解决基于文本的检索方式存在的问题。
图像的特征描述是基于内容图像检索的核心内容, 特征描述的好坏直接影响到图像检索的最终效果。本文通过机械设计图像的特征描述方法的研究, 提高了机械设计图像检索的性能。由于机械设计图像一般为二值图像且图像的纹理信息并不明显, 因此需要从基于形状的角度对机械设计图像的特征描述进行研究。现有的形状描述方法在对机械设计图像进行表示时存在描述不够准确或难以计算的问题, 通过对图像的若干简单几何特征进行研究, 提出一种基于几何特征组合的形状描述符, 能够提高机械设计图像检索的性能。
良好的形状特征描述是图像检索得以进行的必要条件, 形状特征描述需要满足独特性、几何不变性、灵敏性等特点[2]。目前在研究中倾向于将形状特征描述法分为两类:基于轮廓的特征描述法和基于区域的特征描述法。基于轮廓的特征描述法利用目标形状的边界信息进行特征表示, 而基于区域的特征描述法将整个形状区域作为一个整体, 特征表示用到区域内的所有像素。
基于轮廓的形状描述法主要有:链码[3]、曲率尺度空间[4]、傅里叶描述符[5]等。
(1)链码:利用带有一定长度与方向的直线段描述目标的边界。由于每个线段长度固定且方向的数目有限, 所以只需要对边界起点的坐标进行表示, 通过这种方式使用于边界表示所需的数量得以减少。
(2)曲率尺度空间(Curvature Scale Space, CSS):对轮廓图像按照不同的尺度进行高斯平滑, 根据平滑图像中曲率为0的点获得CSS图像, 最后得到CSS曲线的局部最值表示形状。
(3)傅里叶描述符(Fourier Descriptors, FD):主要思想是用图像的边界点通过频域变换后得到的参数(即傅里叶相关系数)对形状进行描述, 经过归一化后的傅里叶描述符具有平移和缩放不变性。
基于区域的形状描述方法主要包括各种基于不变矩和正交矩等的特征描述, 包括Zernike矩[6]、Flusser矩[7]和Hu不变矩[8]等。
(1)Zernike矩是一种正交矩, 能够得到冗余性较小的形状特征, 而且其满足旋转不变性, 同时还具有易构造高阶矩的优点, 经过一定的变换可以使其满足缩放和平移不变性。
(2)Flusser矩包含9个仿射不变矩, 常用来描述从图像中检测到的仿射不变区域, 对仿射变换具有一定的鲁棒性。
(3)Hu不变矩主要思想是利用归一化的二阶和三阶中心矩计算得到的7个对变换不敏感的不变矩, 来表示图像的形状。该特征具有平移、旋转和缩放不变性。
现有的形状特征描述方法在各个领域图像的检索中都得到应用, 并取得了较好的效果, 但针对机械设计图像时, 仍存在较多不足之处。
(1)由于机械设计图像的轮廓细节处常出现畸变现象, 因此链码、傅里叶描述符等基于轮廓的描述方法容易受此影响导致对形状描述不够准确。
(2)形状特征的提取主要是对图像像素的计算, 因此图像形状特征提取效率一定程度上会受图像尺寸的影响。机械设计图像主要是由机械设计图纸按原始尺寸通过扫描输入到计算机中获得, 尺寸普遍较大, 因此部分要求复杂计算的形状特征描述方法如Zernike矩、CSS等, 在机械设计图像形状特征提取过程中效率不高。
几何特征是描述图像形状的简单几何性质的形状特征, 其特征长度为1。机械设计图像形状区域的密实度、矩形度、离心率等几何特征可以通过形状区域的面积、周长等信息较快速地获得, 同时受轮廓的畸变影响较小且具有缩放、平移等不变性, 因此可以用于对机械设计图像进行描述。然而, 由于几何特征描述只用一个数值来表示形状, 单一的几何特征在检索中无法很好地将不同类型的图像区分开。本文利用特征组合的思想, 对机械设计图像中易于计算的几何特征进行研究, 通过分析其特性, 将机械设计图像的7个几何特征进行组合形成形状特征描述符。
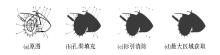
一幅典型的机械设计图像可以分为标引和机械设计主体两个部分, 如图1所示:
由于本文主要从机械设计图像的整体形状上对其形状特征进行描述, 因此机械设计图像中的标引和机械设计主体内部的复杂内容等与整体形状无关的信息会对形状特征的描述造成较大的干扰。因此在进行机械形状特征提取之前, 首先需要对机械设计图像进行形状区域提取。
本文利用孔洞填充[9]、图像形态学腐蚀和膨胀操作[10]和二值图像轮廓跟踪[11]相结合的方法, 对机械设计图像的形状区域进行提取, 大致过程如图2所示:
对机械设计图像的形状特征提取是针对机械设计图像形状区域或其对应的轮廓进行, 从而避免了标引和机械设计内部孔洞区域对形状特征描述的影响。
几何特征可以分为绝对特征和相对特征两种[12]。同一个形状的绝对特征会因其比例的不同而产生变化, 如周长、面积等; 形状的相对特征可以通过绝对特征计算得到, 一般满足旋转、平移或缩放不变性, 如矩形度、圆形度等。由于形状特征描述需要满足各种变换不变性需求, 因此绝对特征不适用于描述机械设计图像的形状; 另外, 相对特征的长度都只有一维, 在形状描述的时候区分性较弱。本文将机械设计图像的7个几何相对特征进行组合, 形成几何特征组合描述符(Combined Geometrical Features Descriptor, CGFD), 加强了形状描述的区分性。由于各个特征分量都比较容易通过计算得到, 因此CGFD的提取易于实现。
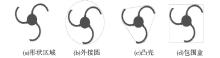
利用机械设计图像的形状区域, 可以得到对应的三个形状描述, 即外接圆、凸壳和包围盒。其中, 形状的外接圆指以形心为圆心, 形状区域上到形心的最远距离为半径的一个圆; 形状的凸壳指能够将形状区域内所有像素都包含在内的最小凸多边形; 形状的包围盒即指形状区域的最小外接矩形。图3分别给出一个形状区域图像对应的外接圆、凸壳和包围盒。
本文机械设计图像的目标像素为黑色(0), 背景像素为(255), 与大部分图像处理理论中的描述正好相反, 因此在进行形状特征提取之前, 首先对形状区域图像的表示函数f(x, y)进行如下定义:
f(x, y)=1 点(x, y)为目标像素
0 点(x, y)为背景像素 (1)
对于一幅机械设计图像f(x, y), 利用其形状区域以及对应的形状描述, 可得到如下形状的绝对特征:
(1)外接圆半径Radius_Cir。
(2)外接圆面积CirArea, 计算方法如下:
CirArea=π × Radius_Cir2 (2)
(3)凸壳面积ConvexArea, 由形状凸壳包含的像素个数近似得到。
(4)包围盒的长BoundBoxLength, 宽BoundBoxWidth, 其中令BoundBoxWidth>BoundBoxLength。
(5)形状区域面积ShapeArea, 用形状区域包含的像素点个数近似计算。
(6)形状区域周长ShapePerimeter, 用形状区域对应的轮廓点个数近似计算。
(7)形状轮廓上的点到质心的最短距离:MinContourDistance。
(8)根据公式(3)计算形状区域对应的三个二阶中心矩u11, u02, u20, 其中(x0, y0)为形状区域的质心[8]。
upq=∑ ∑ (x-x0)p(y-y0)qf(x, y) (3)
根据得到的绝对特征, 可以通过计算得到一系列几何相对特征, 从中选择7个特征, 并为每个特征分量赋予相同的权重, 构成CGFD。设图像对应的CGFD特征向量为F(f1, f2, f3, f4, f5, f6, f7), 则f1-f7分别对应如下7个几何相对特征:
(1)f1:密实度, 指形状区域和凸壳面积比, 表示形状区域上像素分布的紧凑程度。
Solidity=ShapeAreaConvexArea (4)
(2)f2:矩形度, 指形状区域和包围盒的面积比, 表示形状区域对其最小外接矩形的填充程度。
RectRatio=ShapeAreaBoundBoxLength× BoundBoxWidth (5)
(3)f3:形状区域及其外接圆面积比, 表示形状区域对外接圆的填充程度。
CircleRatio=ShapeAreaCirArea (6)
(4)f4:形状周长-面积比, 在一定程度上反映了形状区域对应轮廓的复杂程度。
PeritoArea=ShapePerimeterShapeArea (7)
(5)f5:质心最短距离-质心最长距离比, 一定程度上反映出形状轮廓像素分布的范围。
MintoMax=MinContourDistanceRadius_Cir (8)
(6)f6:包围盒长宽比, 表示形状的狭长程度。
LengthtoWidth=BoundBoxLengthBoundBoxWidth (9)
(7)f7:离心率, 表示形状区域中次短轴向和最大轴向的比值[13]。
e = (u20-u02)2 + 4u211(u20 + u02)2 (10)
根据形状特征描述的分类方法, 可以将f1, f2, f3, f6, f7看成是对形状区域的描述, 将f4, f5看成对形状轮廓的描述。对于CGFD的特征分量f1-f6, 由公式(4)到公式(9)的定义可知:每个特征分量的描述对象都是图像中的目标区域, 因此和形状区域在图像中的位置无关, 满足平移不变性; 每个特征分量均是图像中某两项绝对几何特征的比例关系, 这些比例关系不会因为图像形状区域的旋转发生变化, 满足旋转不变性; 若对图像形状区域进行缩放, 则比例关系中的绝对特征分量会发生等比例的缩放, 对应的特征分量不会发生变化, 满足缩放不变性。对于特征分量f7, 根据文献[13]的描述可知其亦满足旋转、平移和缩放不变性。因此, 一幅图像的CGFD特征不会因为其形状区域发生旋转、平移或者缩放而产生变化。
从以上描述可以看出, CGFD各个特征都能比较容易得到, 而且特征向量的每个分量的值都在[0, 1]之间, 因此无需再进行归一化的操作。对图4中的两类共6幅形状区域图像进行CGFD提取, 得到结果如表1所示, 其中Distance对应的列为各幅图像和图像0之间根据CGFD计算得到的欧氏距离。根据图4和表1可以看出, 虽然部分几何特征单独描述形状时不能很好地区分出两类图像, 如f4和f7。但通过CGFD的7个几何特征组合, 加大了两类图像间的差异性, 实现了对不同形状区分性的提高。
| 表1 CGFD特征提取结果 |
为验证本文提出的几何特征组合描述法在图像检索中的有效性, 在同一个机械设计图像库中利用本文方法和现有的图像检索方法进行检索实验并进行对比。在众多图像检索方法中, 基于Hu不变矩和傅里叶描述符的方法在各个领域的图像检索中得到广泛的应用并取得较理想的效果, 将它们应用于机械设计图像检索得到的结果具有一定的代表性和可比性, 因此选取这两种方法作为实验的对比对象。
Hu不变矩是一种基于区域的形状描述符, 在检索实验中根据文献[8]对形状区域中所有像素计算得到图像的7个不变矩作为其Hu不变矩特征; 傅里叶描述符是一种基于轮廓的形状描述符, 因此在形状特征提取之前需要对形状区域进行边缘检测得到相应的轮廓, 并将边界点根据公式(11)映射到复平面空间, 其中(x, y)表示边界点在原始图像中的坐标, 再根据f(t)按文献[5]所述方法计算得到一系列归一化的傅里叶系数, 在检索实验中取前256项系数作为图像的傅里叶描述符。
f(t)=xt+ jyt t=0, 1, 2, … N-1 (11)
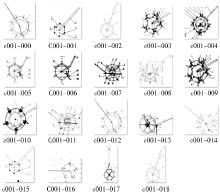
本文的机械设计图像库总共包含2 543幅机械设计图像, 图像库主要分为两个部分:第一部分为已分类图像, 其中含有15个类共441幅图像, 图像类按c001, c002, … , c015的形式命名; 第二部分为未分类图像, 共2 102幅。表2为15个类对应的图像数, 图5为图像库中c001类下的所有图像。
| 表2 15个图像类中包含的图像数 |
具体的实验方法如下:.
(1)提取机械设计图像库中所有图像对应形状区域的CGFD特征、Hu不变矩特征以及FD特征, 构成图像特征库。
(2)将机械设计图像库中15个已分类图像下的所有图像作为输入图像分别进行检索, 并利用欧氏距离来衡量图像间的相似性。统计每个类中三个方法的平均查准率和查全率, 根据平均查准率和查全率绘制对应的查准率-查全率曲线。
(3)设待查询图像的个数为N, 将第j幅待查图像在返回结果数为i时的查准率记为Pi(j), 根据i=10, 20, 30, 40, 50的情况下计算各个检索方法的平均查准率, 方法如下所示:
APi=∑ Nj=1Pi(j)N (12).
(1)分类检索性能结果比较及分析
根据检索结果可以得到15个类在三种检索方法下的平均查准率-查全率曲线, 如图6所示(结果按从左至右, 从上至下升序排列)。
先将CGFD与Hu不变矩进行检索性能比较, 可以看出:CGFD在c012类中的检索效果不如Hu不变矩, 在c005, c006等6个类下的检索效果有明显的提高, 在其余类的检索中二者的效果相当。再将CGFD和FD进行检索性能比较, 可以看出:CGFD在c001, c013和c015这三个类中的检索效果与FD相当, 在其余的12个类中的检索效果都优于FD。
(2)图像检索精确度结果比较
根据公式(11)计算所有图像的平均查准率, 计算结果如表3所示, 可以看出, 在不同的返回结果集下, 其平均查准率与基于Hu不变矩和FD的检索方法相比, 都有较大的提高。
| 表3 三种检索方法的平均查准率 |
本文从基于形状的特征描述上研究如何改进机械设计图像检索效果, 提出一种由形状的7个几何特征组合构成的形状描述符, 该特征易于计算而且无需归一化。实验结果表明, 在机械设计图像检索中, 基于本文方法的检索查准率-查全率性能相较于FD和Hu不变矩有所提高。通过比较不同结果集下的平均查准率表明该方法在检索的精确度上相比于FD和Hu不变矩有较大的提高。然而, 该方法在不同类别的机械设计图像检索中, 其检索效果差异较大, 稳定性不足, 因此今后应该对形状特征描述方法进行更深入的研究, 通过既稳定又高效的特征表示方法, 进一步提高机械设计图像的检索性能。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|