[
引用本文
沈耕宇, 黄水清, 王东波. 以作者合作共现为源数据的科研团队发掘方法研究. 现代图书情报技术, 2013, 29(1): 57-62
Shen Gengyu, Huang Shuiqing, Wang Dongbo. On the Scientific Research Teams Identification Method Taking Co-authorship of Collaboration as the Source Data. New Technology of Library and Information Service, 2013, 29(1): 57-62   
Permissions
以作者合作共现为源数据的科研团队发掘方法研究
沈耕宇, 黄水清, 王东波
南京农业大学信息科学技术学院 南京 210095
摘要
在对个人和科研机构的评价研究中, 针对难以准确、可靠地界定与识别科研团队的问题, 将向量空间模型应用到作者合著关系网络的科研团队发掘研究中。在考虑论文作者署名顺序的前提下, 构建论文与作者向量空间, 通过计算作者向量的相似度来衡量作者之间的合作关系, 再通过社会网络分析中的凝聚子群分析方法分析作者合作关系网络。最后, 以某高校内某学院的所有在编教师为研究对象, 准确地发掘出所有真实存在的科研团队, 从而验证方法的合理性。
关键词: 向量空间模型; 作者合作相关度; 派系分析; 科研团队发现; 合著关系网络
On the Scientific Research Teams Identification Method Taking Co-authorship of Collaboration as the Source Data
Shen Gengyu, Huang Shuiqing, Wang Dongbo
College of Information Science and Technology, Nanjing Agricultural University, Nanjing 210095, China
Abstract
In the research on personal and institutional evaluation, it is difficult to guarantee the reliability and accuracy of identifying the scientific research team.This paper applies the vector space model into the identification of scientific research teams within the co-authorship network. Under the premise of considering the authorship order in the paper, and by constructing the vector space of papers and authors, the collaboration relationship is measured by calculating the degree of similarity between author vectors. Then, this paper analyses the collaboration network with the analytical approach of cohesion sub-group in social network analysis. At last, by choosing all its faculty of a department in a university as research object, the present research accurately identifies all the scientific research teams that exist in the institution and the rationality of this method is verified.
Keyword: VSM; Degree of collaboration between authors; Cliques analysis; Mining of the scientific research team; Co-authorship network
引 言

同一学术机构尤其是高校内存在着广泛的科研合作, 由科研合作关系产生固定的科研团队, 而科研团队的准确界定与识别, 对于个人与学术机构的评价都至关重要。在以往的个人与机构的评价研究中, 并没有一种行之有效的方法准确界定科研团队。社会网络分析方法(Social Network Analysis, SNA)的引入在一定程度上改变了科研合作网络的研究状况。学术机构内科研合作的显著表现形式是研究人员合作发表论文。在传统的合著关系网络
的构建过程中, 作者署名的共现频次往往作为衡量作者之间合作程度的标准, 但是这一指标没有考虑作者署名顺序的不同所代表的作者对论文贡献程度的不同。由于忽视了不同作者对论文的贡献程度的差异[1], 因此导致从论文合著关系网络中发掘和界定科研团队的不准确和不合理。为了准确识别一个学术机构内真实的科研合作团队, 本文在作者署名共现分析的基础上考虑作者的署名顺序, 分析合著论文中作者之间的合作相关度; 使用向量空间模型算法计算作者间相互合作的程度, 对由此构建的合著关系网络使用社会网络分析方法分析, 以便能够准确界定机构内的科研团队。本文为个人和机构评价中的合作团队的界定提供了合理有效的方法, 从而在一定程度上保证了个人与机构评价的准确与客观。

2 相关研究现状

近年来, 针对科研合作的研究, 网络分析方法正逐步取代传统文献计量的分析方法, 并被应用于科学评价的研究中, 其中有研究人员提出将合作网络分析作为社会科学学科评价研究的具体方法[2]。科研团队的界定作为科学评价的一部分, 国内外研究人员纷纷研究具体领域的合著网络, 针对其中合作团队的结构特征开展分析[3, 4, 5, 6, 7, 8]以发现真实的科研团队。Leung等[9]开发了一套工具, 用于对合著网络进行可视化分析, 在可视化技术生成的合著网络中发掘科研团队。Han等[10]提出一种基于作者合作支持度分析的方法, 计算合著网络中作者之间的合作程度, 并设计了一套从合著网络中发掘团队的算法。Gregorio等[11]对有关南美锥虫病研究的论文合著网络进行社会网络分析, 发现了该研究领域中的科研合作团队。

随着社会网络分析方法被广泛应用于合著网络的分析研究当中[12], 国内的研究人员在学术机构、学术领域、研究热点等方面, 均尝试使用社会网络分析方法分析合著网络。李亮等[13]利用社会网络分析方法对情报学领域的作者合作关系网络进行分析, 基于小团体分析方法, 发现了合著网络中联系紧密的小团体, 指出合著网络中核心作者的数量和所属机构。邱均平等[14]利用社会网络分析法对国内文献计量学领域的作者合著网络进行研究, 为明晰文献计量学领域的知识交流模式和发现潜在的合作团体提供了一定的参考。余丰民等[15]在对情报学领域高产论文的作者合著网络进行可视化构建的基础上, 分析了重要合作团队的形成机制。庞弘燊等[16]以大连理工大学WISE实验室为样本, 结合社会网络分析方法研究科研团队内部的作者合作紧密程度。

3 研究方法

向量空间模型的向量相似度的计算, 为作者之间的合作相关度计算提供了思路。基于期刊论文的作者共现和署名排序信息构建论文与作者向量空间, 由此计算出作者之间合作的相关度, 为科研团队的挖掘提供准确的数据依据。

3.1 作者与论文的向量空间表示

在论文作者关系向量中, 首先要将存在论文合作关系的作者通过向量来表示, 作者之间通过论文合著产生关系。每一篇论文中的作者署名的信息代表了论文与作者之间关系, 论文作者与论文的关系类似关键词与文章的关系, 根据文档的向量空间表示方式, 可以利用论文的作者署名信息构建作者向量。每一个作者独立构成了一个作者向量Aj=(ai1, ai2, … , aij, … , ain)T, aij表示第j个作者在第i篇论文中的权重。其中aij的权值由作者的署名顺序和是否为通讯作者决定, 权值的定义如下所示[17]:.

aij=1 作者j是论文i的第一作者或通讯作者
1k 作者j是论文i署名中排第k位的作者, 但不是第一作者和通讯作者
0 作者j不是论文i署名中的作者 (1).

作者的署名顺序可以反映出作者对该篇论文的贡献程度, 作者向量的分量对应于在每篇论文内作者署名排序信息, 排在第一位的第一作者和论文的通讯作者, 一般对论文的贡献程度比较高, 所以权值均为1, 排在其他位置的作者在论文中权重为其排序的倒数, 例如论文中第二位的作者权重为0.5, 第三位的作者权重为0.333, 权重按署名排序依次递减。

由上述作者向量构建过程可知, 在考虑论文作者对论文贡献程度不同的前提下, 作者与作者的合作相关程度的计算, 可以转化成在相关性矩阵中计算作者与作者向量的相似度, 由此构建的论文作者的相关性矩阵如图1所示。
作者/论文 D1 … Dj … Dn
A1

Aj

Am a11… a1j… a1n
  
ai1… aij… ain
  
am1… amj… amn
图1 作者与论文相关性矩阵.

作者论文关系矩阵是一个m× n阶的矩阵, m表示m位合作作者, n表示合著的论文总数。矩阵的行Am表示由作者的论文署名信息映射得到的作者特征向量, 矩阵的列Dn表示一篇论文中的所有作者权重向量。

3.2 作者的合作相关度计算

为了计算作者向量之间的相似度, 需要作者与论文关系的向量空间模型。作者向量相似度的计算使用向量夹角余弦系数法。从作者权重的计算公式来看, 存在每篇论文的作者权重的平方和偏离1的现象。在进行向量相似度计算之前, 需要对作者向量中的分量数据进行归一化处理。归一化处理后得到作者向量B=(bi1, bi2, … , bij, … , bin)T, 其中bij的定义如下:
bij=aij∑ Nj=1a2ij (2).

其中, aij表示作者在论文中根据署名顺序得到的权重, 将归一化后的作者向量再次构造出作者与论文的相关性矩阵, 如图2所示:
B=b11b12… b1j… b1n
  
bi1bi2… bij… bin
  
bm1bm2… bmj… bmn
图2 数据归一化后的作者与论文相关性矩阵.

经过归一化数据处理创建的作者与论文相关性矩阵也是m× n阶的矩阵。根据向量夹角余弦的计算公式, 作者合作相关度的计算公式定义如下[18]:.

sim(Bi, Bj)=cosθ =∑ nk=1bik× bjk∑ nk=1(bik)2× ∑ nk=1(bjk)2 (3).

由公式(3)计算出的向量Bi与Bj的相似度值, 体现了作者Bi与Bj在所有论文中的合作相关程度。由此又可以构建作者与作者的合作相关性矩阵, 该矩阵与作者共现分析的合作频次矩阵的差别在于, 作者之间的合作相关性是通过更为合理的指标衡量, 而不再是简单的共现频次统计。将向量空间模型引入到作者与论文的关系表达中, 作者在论文合作中的相关性可以充分考虑不同作者对论文的贡献程度。明确作者之间的合作相关度是为了准确地挖掘科研团队, 分析团队内部的合作情况。

4 基于作者合作相关度的科研团队发掘

实例.

选择国内某研究型大学的一个学院作为对象, 将学院内在编教师作为作者集合, 通过构建学院内教师之间的合作相关度矩阵, 利用UCINET中NetDraw工具[19]绘制作者合作相关度网络, 发掘学院内教师中的真实的科研团队及其合作情况。

4.1 数据来源

本文的合作相关度网络, 是依托作者的合作相关度矩阵构建的。构建作者相关度矩阵, 需要作者信息和作者已发表的所有论文作为数据来源。本文选择的是一个学院中的所有在编教师, 将这些教师发表的论文数据作为数据分析的来源。鉴于学院内教师中的科研成果, 多发表在具有世界权威和高影响力的学术期刊上, 在论文数据来源的选择上, 首选ISI中的引文索引数据库Web of Science。在此数据库中检索该学院内83名在编教师2001年到2011年发表的全部论文, 下载数据并经过人工甄别, 共得到548篇论文。再对学院内的83名在编教师依次编号:A1-A83, 用于代替原始文献中的作者信息, 以避免署名不一致造成的错漏。在对数据进行计算之前, 每篇论文、每条作者信息都经过人工检查, 确保数据的真实准确。

4.2 构建作者合作相关度网络

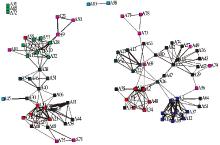
对上述83位教师的论文数据进行过滤和整理后, 构建一个基于作者合作相关度的合作关系网络。首先利用Java语言编写统计作者署名共现频次和计算作者间合作程度的程序; 然后通过程序分别生成83位作者的论文数据的合作相关度矩阵, 将这个矩阵导入UCINET; 最后利用可视化绘图工具NetDraw绘制出作者合作相关度的网络, 如图3所示。

图3 作者合作相关度网络

.

其中, 作者合作关系网络图的节点分别表示83位教师, 节点间连线表示教师之间的合作强度, 而节点之间的连线粗细则表示教师之间的合作相关度, 教师之间的合作相关度越高, 其间的连线越粗。

可以看出, 所有教师的合作相关度网络所展现出的网络的连通性较好, 大多数节点都有与之相连接的节点, 这说明学院内的教师科研合作较为紧密和广泛。图3中的网络被独立地分成三个不相连接的子网, 其中两个子网的规模较大, 节点的个数也大体相当, 第三个子网则只有两个节点, 说明这两位教师只在相互之间存在合作。除了这些多个节点组成的子网, 还有三个不构成网络的独立节点(A31、A65、A72), 说明这三个节点所代表的教师与学院内的其他教师不存在科研合作关系。原因是这三位教师很少发表学术论文, 所以在团队发掘中将这三个节点排除在外。在作者合作相关度网络的两个规模较大的子网中, 网络节点聚集比较紧密, 并且分别存在几个关键的枢纽节点, 这些枢纽节点连接了合作关系紧密的其他子网。这也意味着学院内有些教师的合作范围, 不仅仅局限在自己的科研团队内, 同时还与其他团队有交叉合作。

由图3还可以看出, 合作紧密的教师数量分布均匀, 从结构上体现出一种社会网络中的小团体凝聚的现象, 间接反映了科研合作中的团队合作情况, 从某种意义上说明, 对合作相关度网络的进一步分析, 能够为科研团队的发现和研究提供帮助。

4.3 合作相关度网络中科研团队的发现与分析

(1)合作相关度网络中的凝聚子群分析.

对教师合作相关度网络的结构分析发现, 该网络中某些节点之间的关系特别紧密, 以至于这些节点结合成为一个个次级的小团体, 在社会网络分析中, 网络的这种特征被称为凝聚子群。合作相关度网络中的凝聚子群体现了教师之间的团队合作的特征, 社会网络分析中的凝聚子群分析的主要目的, 就是发现网络中存在多少这样的子群。凝聚子群的分析方法可以准确地测度出网络中有较强的、直接的、紧密关系的小团体, 因而对教师合作相关度网络进行凝聚子群分析, 可以发现密切合作的子群即潜在的科研合作团队。

社会网络分析的凝聚子群分析也被称为“ 小团体分析” , 科研合作团队在作者合作相关度网络中也是以小团体聚集的形式体现。使用凝聚子群分析作者合作相关度网络, 选择凝聚子群分析中派系分析方法, 本文使用UCINET工具中的n-cliques(n-派系)分析功能。n-cliques分析是计算网络中在n个节点范围内所构成的小团体, 在教师合作相关度网络中选定n为2, 因为小团体的节点数至少为2才能进行派系分析。总共划分出25个小团体, 如表1所示:

表1 论文作者合作相关度网络的派系划分
利用凝聚子群划分的教师合作小团体中, 分析出的25个派系中有些成员与许多派系的成员合作频繁, 例如多个派系都包含A1、A2、A3、A5、A6、A18几位教师, 说明这几名教师在划分出的团队中都是团队的核心成员, 并且在各自的派系中充当重要枢纽的作用, 这些教师多起着领导整个团队的作用。从划分的派系中发现, 教师合作团队中有些团队人数众多, 有些团队的人数较少, 人数较多的团队基本上属于某一学科的重点实验室或者一些重大项目课题组, 这说明作者合作相关度网络的派系分析真实地反映了实际科研团队合作情况。

(2)通过凝聚子群分析发现的科研团队.

基于作者合作相关度网络的凝聚子群分析, 划分出10个派系, 即10个可能的科研合作团队, 并通过凝聚子群分析中的n-派系分析得到层次聚类图, 如图4所示:

图4 作者合作相关度层次聚类图

.

结合以上层次聚类树状图中的聚类结果和表1的派系划分筛选出新的10个派系如表2所示。在此基础上, 得到学院内部的科研合作团队。

表2 学院内教师科研团队派系划分
在表2列出的教师合作团队划分结果中, 出现了某些教师交叉合作的团队, 团队1和团队8中的部分教师在两个团队中都分别参与了各团队的科研合作, 此时便可根据团队成员之间的合作相关度探究成员之间的真实的合作关系。首先从划分出的科研团队中寻找出核心人员, 从图3的网络图中可以看出, 团队1中的核心研究人员是A5, 团队8中的核心研究人员是A30。在团队1中A5、A8和A20所代表的教师与团队核心成员的相关度较高, 而在团队8中这三位教师分别与团队核心成员的合作相关度却比团队1中低了一个数量级, 具体的相关度对比如表3所示, 因此将A5、A8、A20三位教师划分到团队1中更合理。
表3 A5、A8、A20分别与团队核心成员的合作相关度
虽然一些教师在两个不同团队中均参与了科学研究, 并合著过一些论文, 但由于教师在不同团队中相互合作程度不同, 导致其在不同科研团队中的参与程度存在差异, 这对于分析科研团队的组成结构很有帮助, 而这些特性在简单的署名共现的合著网络中是难以察觉的。

5 结 语

本文借鉴向量空间模型, 根据不同作者在合著论文中署名顺序的不同, 构建作者和论文关系矩阵, 用于挖掘科研团队。在实例研究中, 计算某高校一个学院内教师之间的合作相关度, 使用社会网络分析方法中的派系分析方法并结合作者的合作相关度将学院内的教师划分为10个科研合作团队。未来除了进一步对作者合作相关度进行深入分析外, 还可以将本文的方法用于关键词的相关性分析, 以期能从中发现潜在的研究方向和研究热点。

参考文献
[1] Tscharntke T, Hochberg M E, Rand T A, et al. Author Sequence and Credit for Contributions in Multiauthored Publications[J]. PLOS Biology, 2007, 5 (1) : 13-14. [本文引用:1] [JCR: 11.452]
[2] 瞿辉. 基于合作网络分析的社会科学评价研究[J]. 评价与管理, 2011, 9 (3) : 45-48. (Zhai Hui. Study on Evaluation of the Social Sciences Based on Co-authorship Network Analysis[J]. Evaluation & Management, 2011, 9 (3) : 45-48. ) [本文引用:1]
[3] Acedo F J, Barroso C, Casanueva C, et al. Co-authorship in Management and Organizational Studies: An Empirical and Network Analysis[J]. Journal of Management Studies, 2006, 43 (5) : 957-983. [本文引用:1]
[4] Liu X M, Bollen J, Nelson M L, et al. Co-authorship Networks in the Digital Library Research Community[J]. Information Processing and Management, 2005, 41 (6) : 1462-1480. [本文引用:1] [JCR: 1.119]
[5] Long J C, Cunningham F C, Braithwaite J. Network Structure and the Role of Key Players in a Translational Cancer Research Network: A Study Protocol[J]. BMJ Open, 2012, 2 (3) : 1-8. [本文引用:1]
[6] 荣先乾, 覃桃. 社会网络分析方法在图情领域合著关系的实证研究[J]. 图书馆界, 2010 (1) : 1-5. (Rong Xianqian, Tan Tao. An Empirical Study on Co-authorship Analysis in the Field of Library and Information Science with Social Network Analysis[J]. Library World, 2010 (1) : 1-5. ) [本文引用:1] [CJCR: 0.4715]
[7] 周玉芳. 基于社会网络分析的我国学科服务研究的主要学术合作群体和热点研究[J]. 现代情报, 2012, 32 (3) : 49-53. (Zhou Yufang. The Main Co-authorships and Hotspots of Subject Service in China Based on the Social Network Analysis[J]. Modern Information, 2012, 32 (3) : 49-53. ) [本文引用:1] [CJCR: 0.7683]
[8] 李纲, 李昂. 基于社会网络分析的学术团体合著研究— — 以武汉大学计算机学院为例[J]. 信息资源管理学报, 2011, 1 (3) : 43-47. (Li Gang, Li Ang. Study on Co-authorship of Computer School in Wuhan University Based on Social Network Analysis[J]. Journal of Information Resources Mangement, 2011, 1 (3) : 43-47. ) [本文引用:1]
[9] Leung C K S, Carmichael C L, Teh E U. Visual Analytics of Social Networks: Mining and Visualizing Co-authorship Networks[C]. In: Proceedings of the 6th International Conference on Foundations of Augmented Cognition: Directing the Future of Adaptive Systems. 2011: 335-345. [本文引用:1]
[10] Han Y, Zhou B, Pei J, et al. Understand ing Importance of Collaborations in Co-authorship Networks: A Supportiveness Analysis Approach[C]. In: Proceedings of the SIAM International Conference on Data Mining. 2009: 1111-1122. [本文引用:1]
[11] Gregorio G, Jinseo P, Charles H, et al. Scientific Authorships and Collaboration Network Analysis on Chagas Disease: Papers Indexed in Pubmed (1940-2009)[J]. Journal of the Institute of Tropical Medicine in Sao Paulo, 2012, 54 (4) : 219-228. [本文引用:1]
[12] 邱均平, 吴菲菲. 基于SNA的国内竞争情报领域作者合作关系研究[J]. 图书馆论坛, 2010, 30 (6) : 34-40. (Qiu Junping, Wu Feifei. Reasarch on the Author’ s Collaboration Relationships of the Domestic Competitive Intelligence Field Based on Social Network Analysis[J]. Library Tribune, 2010, 30 (6) : 34-40. ) [本文引用:1] [CJCR: 1.2118]
[13] 李亮, 朱庆华. 社会网络分析方法在合著分析中的实证研究[J]. 情报科学, 2008, 26 (4) : 549-555. (Li Liang, Zhu Qinghua. An Empirical Study of Coauthorship Analysis Using Social Network Analysis[J]. Information Science, 2008, 26 (4) : 549-555. ) [本文引用:1] [CJCR: 0.8488]
[14] 邱均平, 伍超. 基于社会网络分析的国内计量学作者合作关系研究[J]. 图书情报知识, 2011 (6) : 12-17. (Qiu Junping, Wu Chao. Study on the Co-author Relationship of Informetrics Based on Social Network Analysis[J]. Document, Information and Knowledge, 2011 (6) : 12-17. ) [本文引用:1]
[15] 余丰民, 汤建民. 情报学领域较大规模合著网络的可视化识别及其形成机制研究[J]. 情报理论与实践, 2011, 34 (8) : 41-46. (Yu Fengmin, Tang Jianmin. Visualized Identification and Formation Mechanism of the High-yield Co-authorship Network in the Information Science Field[J]. Information Studies: Theory & Application, 2011, 34 (8) : 41-46. ) [本文引用:1] [CJCR: 0.9514]
[16] 庞弘燊, 方曙, 杨波, 等. 科研团队合作紧密度的分析研究— — 以大连理工大学WISE实验室为例[J]. 图书情报工作, 2011, 55 (4) : 28-32. (Pang Hongshen, Fang Shu, Yang Bo, et al. Research on the Close Degree of Cooperation in Research Team— An Empirical Study in WISE Laboratory in Dalian University of Technology[J]. Library and Information Service, 2011, 55 (4) : 28-32. ) [本文引用:1] [CJCR: 1.0423]
[17] 孙丽娟. 科技论文作者署名排序与通讯作者[J]. 中国科技期刊研究, 2005, 16 (2) : 242-244. (Sun Lijuan. Authorship Order and Corresponding Author of Scientific Papers[J]. Chinese Journal of Scientific and Technical Periodicals, 2005, 16 (2) : 242-244. ) [本文引用:1] [CJCR: 0.9855]
[18] Salton G, Wong A, Yang C S. A Vector Space Model for Automatic Indexing[J]. Communications of the ACM, 1975, 18 (11) : 613-620. [本文引用:1] [JCR: 1.919]
[19] UCINET 6 for Windows Software for Social Network Analysis [EB/OL]. [2012-12-10]. http: //www. analytictech. com/ucinet/help. htm. [本文引用:1]