从数据降维的角度来看,传统共词分析中以高频词构建共词矩阵的方法有较大的改进空间。将共词分析与文本分类、聚类、检索等方法进行对比归一,引入词语贡献度作为新的特征词选择方法,并给出算法描述。从聚类效果层面将新方法与传统方法进行对比,通过实证验证基于词语贡献度的特征选择方法对共词分析有改进作用。
From the view of data dimension reduction, the method of constructing co-word matrix by high frequent words has a great improvement space. By comparing co-word analysis with traditional text processing including text categorization, text clustering and information retrieval, the authors introduce a new feature selection method based on term contribution and the algorithm description. Through experimental comparison, it is shown that the new method has obvious effect on improving the data quality and cluster result.
共词分析中为聚类而构建共词矩阵是关键步骤,作为聚类分析的数据输入,共词矩阵的构建应有两方面操作:选择聚类对象,以代表研究领域中的关键知识点;选择特征词,以描述待分析知识点间的关联和差异。传统共词分析方法中,为避免低频词对聚类和可视化效果的干扰,仅截取高频词及它们之间的共现关系来构建共词矩阵。这一做法默认了高频词既能代表共词网络中的关键知识点,又能作为描述共词网络的特征维度。目前已有研究者通过实验验证这些高频核心词可表征核心知识概念[ 1],然而从数据降维的角度来看,以高频词作特征维度的方法最为原始,存在较大的改进空间,其原因是在信息抽取中某些稀有词恰恰更能反映类别的特征,因而不应该被滤除[ 2]。在实际应用中,关键知识点的选择可人工修正,而特征词的选择则完全无法人工判断,因而后一问题更加紧迫,需要引入更合适的特征选择方法予以解决。
共词分析方法中的数据是对称矩阵,其行、列均为代表重要知识点的高频词。共词分析的核心思想是用其他词来描述某词,因而其数据本质上属于<对象,特征>形式的描述型数据。在更广泛意义上的聚类方法中,输入数据为用若干特征所描述的对象集合,对应的矩阵形式为:行表示聚类对象,列表示特征维度[ 3]。用于聚类的共词矩阵也应回归到这一数据形式,即行作为表示重要知识点的聚类对象,列作为表示特征维度的特征词,行列内容各自用更合理的方式来选取。这种更符合聚类本质思想的数据处理方式,是开展共词分析特征选择方法优化的前提。另外,本文参考的文本向量空间矩阵也符合<对象,特征>形式,其行表示文档,列表示特征词。因而在数据模型层面,共词矩阵和文本向量空间矩阵可进行统一,如图1所示,这是在共词分析中引入文本处理领域更成熟特征选择方法的前提。
共词矩阵的构建本质上是进行数据降维。数据降维方法有两类:特征选择,即从原始诸多特征中选择最有代表性的少量特征,组成新的数据空间,这类方法并未改变原空间的特征属性;特征抽取,即对原始特征进行运算,得到一些新类型的特征[ 4]。共词矩阵中的特征维度需要保持词汇形式,因而其降维方法属于特征选择。
目前没有用于共词分析的特征选择方法,但可借鉴文本处理(如检索、分类、聚类)中的特征选择方法[ 5, 6]。根据规则是否依赖于预定的类信息,特征选择方法可分为有监督、无监督两类。有监督的特征选择方法根据预定的类,辅以训练集中提前获得的<特征,文档,类别>关系,其降维效果能在去掉98%的特征词后仍保持较好甚至有所提升[ 7],典型的方法有互信息(MI)、信息增益(IG)、χ2统计(Chi-Square)等[ 6],多用于文本分类;无监督的特征选择方法由于难以提前预定类信息和组织训练集,因而其效果略差,典型的方法有文档频次(DF)、词语贡献度(TC)、单词权(TD)等[ 8],多用于文本聚类。另外,在文本聚类中,有研究者采用以无监督特征选择方法进行聚类后反过来再优化特征选择的方法,实现模拟监督聚类的效果[ 9]。
在以关键词为来源的共词分析中,包含某关键词的文档频次实际上就是其词频,以高频词为特征词相当于使用文档频次方法进行特征选择。虽然目前没有针对共词分析中按词频选择特征词效果的研究,但在文本分类、文本聚类领域中,已有较多研究指出:文档频次方法与互信息、信息增益等方法相比,聚类效果有较大差距[ 1, 9],而共词聚类与文本分类、文本聚类同样是以特征词描述待选对象的聚类方法,因而上述研究从侧面说明单纯依据词频选择特征词存在较大改进空间。
共词分析中无法提前预定类信息,也无法建立训练集,因而难以借鉴有监督的特征选择方法;无监督特征选择方法中:迭代聚类模拟有监督效果的方法因不易操作暂不考虑;文档频次方法等同于共词分析中的高频词选择;词语贡献度、单词权的方法用于文本聚类时效果接近[ 9],相比而言前者逻辑更简单,所采用的tf、idf参数更易引入到共词分析中。
词语贡献度是用来描述词语(Term)对整个数据集相似性的贡献程度,其计算公式如下[ 7]: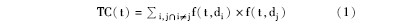
其中,f(t,d)表示词语t在文本d中的权重,即tf-idf值。tf为文档中某特征词出现的频次除以文档集中该特征词的总频次;idf为文档总数除以包含该特征词的文档数再取对数[ 10]。
基于2.1节论述,可将文本处理中基于词语贡献度的特征选择方法引入到共词分析中,对比图1,以高频词作为聚类对象(行),模拟文本向量空间模型中的文档,模拟的文档内容由与该高频词共现过的其他词语组成;以高贡献度词作为特征词(列),模拟文本向量空间模型中描述文档的特征词。在共词矩阵中计算词语贡献度时,tf为某列特征词与某行高频词共现次数除以该特征词的词频,idf为矩阵总行数除以出现该列特征词的行数再取对数。当行和列词语相同时,其tf-idf值需进行初始化,本文设为0,原因是词语在聚类中的贡献表现为它如何描述其他词,而非描述自己。由此,可得出共词分析中特征词的词语贡献度计算公式如下: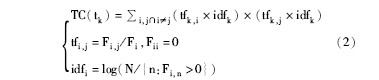
基于词语贡献度特征选择的共词矩阵构建算法包括4步:数据预处理、生成候选特征词矩阵、计算tf-idf值和词语贡献度、生成最终特征词矩阵。其后的聚类分析与传统共词分析方法相同。算法流程描述如下:
①读入关键词文件keyWordFile、停用词表StopWordList和替换词表ReplaceWordMap,剔除和替换完成后得到词频表FrequentMap(<词语,频次>)和共现关系表RelationMAP(<词1 &词2,共现次数>);
②词频表FrequentMap中,读取频次≥m(本文取m=10)的高频词代表重要知识点,作为M个聚类对象行;读取频次≥n(本文取n=3)的词为候选特征词,作为N列。根据RelationMAP中相应词对的共现次数,生成M×N非对称候选特征词矩阵RelationMatrix;
③对RelationMatrix按列和行依次嵌套循环,按公式(2),计算列在行上的tf-idf值,生成tf-idf矩阵TfIdfMatrix。逐列计算各候选特征词针对M个聚类对象的词语贡献度TC值,降序输出词语贡献度表TcMap(<特征词,贡献度>)。截取前 P个词(本文取P=M)作为特征词集TopTcList。
④根据TopTcList,剔除RelationMatrix中非特征词的列,得到最终的特征词矩阵TcRelationMatrix。将其导入数据统计软件中,转化为Pearson相似矩阵,进行聚类。
(注: 1)在步骤②中,由于一篇论文中不会出现相同关键词,故共现频次矩阵RelationMatrix中行、列词相同时,频次本身即为0,无需额外作初始化操作;2)在步骤③中,由于本文后续对比<高频词,高频词>矩阵与<高频词,高贡献度词>矩阵的聚类效果,为公平起见,取与高频词等量的高贡献度词,两个矩阵都为M×M矩阵,实际操作中可根据需要选择特征词数量;3)在步骤④中,Pearson矩阵为对称矩阵,非对称词频矩阵TcRelationMatrix的转化处理,可在Ucinet中选择“Tools-similarities”按rows计算完成;或使用SPSS“分析-相关-双变量”中按Pearson系数计算,但由于SPSS只对原始矩阵的列元素进行相关性计算,为了得到原始矩阵行元素的相关性,需要先对TcRelationMatrix进行转置,再输入SPSS。)
本文以“数字图书馆”领域为研究对象,使用相同的数据来源,分别采用基于词频、词语贡献度两种特征选择方法,构建共词矩阵,作为评估数据。具体方法是:从CNKI中按标题或关键词中是否包含“数字图书馆”检索,从2002年-2012年间发表于该学科领域核心期刊的2 178篇正式论文中提取关键词和共现关系。预处理时,删除意义过于宽泛的词语并进行简单的同义词合并。值得一提的是,理论上,只要人工处理极尽完善,最终得到的聚类结果也会非常合理。但本文关注的恰恰相反,即:采用更合适的特征选择方法,以减少初始数据不规范对分析结果的负面影响。因此只对原始数据进行最粗略的处理,以验证新的特征选择方法是否有效。
处理完成后,共获得关键词2 807个,关键词分布如表1所示:
| 表1 全部关键词词频分布 |
| 表2 等量高频词与高贡献度词集合差异 |
| 表3 TOP75高频词与TOP75高贡献度词集合中差异词 |
迄今为止,由于缺乏有效的量化指标,在对比不同共词分析方法的效果时,研究者通常依据自身知识背景对最终聚类结果进行定性评判。在参考文献[11,12]基础上,本文加入一些简单的量化数据,以便更可靠地验证新的共词分析效果。
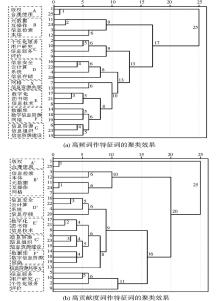
为更清晰简洁地展现聚类效果,同时节省篇幅,取两个矩阵中前25个词的聚类效果进行对比,如图2所示。为便于比较,聚类图中标出了较小的基本聚类单元(同单元内词关系较紧密,且单元内词数均衡在2-5之间),分别为A:版权问题,B:数据模型技术,C:用户服务,D:资源存储问题,E:资源数字化技术,F:数字信息资源,G:信息资源组织建设,X:信息资源共享。聚类图中标出了每个词语、类团完成聚类需要的步数,用于量化地揭示类团间的紧密程度。图2中在10-15步间进行类别切分,可得到4个较清晰无歧义的大类:数字图书馆中的版权问题(单元A)、数据模型(单元B)、用户服务(单元C)、信息资源管理(单元D、E、F、G、X)。
对比图2(a)和图2(b),其聚类单元有一处差异:图2(a)中将网格和信息资源共享聚在一起,图2(b)中将网格与{元数据,互操作}聚在一起。笔者追溯原文献集发现,与网格相关的研究主要在实际应用和技术模型两个方面,前者与信息资源共享关联较多,后者与互操作、本体关联较多。实际上,有较多研究将网格与互操作、元数据等技术词汇归为一类[ 13, 14],本文也更倾向如此。
为避免过多的主观判断,本文通过类团间的聚类步数来对比类团间的差异性、通过类团内聚类步数来对比类团内的紧密程度。图2(a)和图2(b)中,将4个大类团聚类起来的步数为:(a)图{13,17,25},(b)图{16,20,25},因而(b)图中类团间差异性更大。4个大类团内部,聚类完成的步数为:(a)图{1,9,9,13},(b)图{1,10,11,9},在信息资源管理类团内,(b)图中D’、E’、F’、G’、X’几个小单元内部及它们之间的聚类要明显紧凑于(a)图;(b)图中B’单元多1步是因为加入了{网格}一词,C’单元中多2步是因为对{信息服务,用户研究,个性化服务}与{评价}的区分更清楚。相比而言(b)图对于类团内的聚类单元处理更优。
对比TOP25词聚类效果可以看出,依据词语贡献度挑选特征词所构建的共词矩阵,得到的聚类结果中类团间差异性更明显,类团内紧密性更好,因而聚类效果更好。
在共词分析中,与高频词作特征词相比,依据词语贡献度词所选的特征词集有少量词语变化。即便如此,新的共词聚类效果更优,表现为:类团间差异性更明显,类团内关联更紧凑。因此改进特征选择方法可优化共词分析效果,而词语贡献度是其中较为简单有效的一种。
本文从基本的<对象,特征>数据模型出发,提出将共词矩阵中行、列回归到一般意义上的聚类对象、特征维度,以此将共词矩阵与文本处理中已较为成熟的向量空间模型相对应。基于此,后续有两个可供研究的方向:.
(1)纵向角度上,进一步优化共词分析方法。包括特征选择方法优化、共词网络中关键知识点提取两个方面。除词语贡献度外,在文本处理乃至更广泛意义上的数据降维中,有更多可参考的特征选择方法,特别是一些模拟监督效果的无监督特征选择算法[ 9],可供引入。另外,以高频词代表学科领域中的关键知识点这一做法也存在改进空间,因此更合理地从共词网络中提取代表性词语也是一个重要的研究点。
(2)横向角度上,优化基于共现关系的计量分析方法。除共词分析外,包括同被引、作者耦合等在内的诸多计量分析方法对数据的处理较为原始,数据不规范和研究者主观认识会影响到分析结果,如何从大量数据中有效提取分析对象、选择描述特征是这些计量方法科学化、客观化的关键。只有回归到<对象,属性>这一最基本的数据模型,区分用于数据中的分析对象和描述特征,才能有差异性、有针对性地选择优化方法,以引入其他领域成果来改善本学科基础方法。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|