引用本文
石崇德, 乔晓东, 王惠临. 知识组织与知识管理树转录翻译模型解码优化. 现代图书情报技术, 2013, 29(9): 23-29
Shi Chongde, Qiao Xiaodong, Wang Huilin. Decoding Optimization in Tree Transducer based Translation Model. New Technology of Library and Information Service, 2013, 29(9): 23-29  
Permissions
知识组织与知识管理树转录翻译模型解码优化
石崇德, 乔晓东, 王惠临
中国科学技术信息研究所 北京 100038
修回日期:2013-07-22
基金:本文系中国科学技术信息研究所重点工作项目“多语言科技信息语义关联网络构建及其应用” (项目编号:ZD2012-3-3) 和中国科学技术信息研究所学科建设项目“自然语言处理” (项目编号:XK2012-6) 的研究成果之一。
摘要
针对树转录翻译模型中的规则二元化和解码算法进行深入研究, 通过四分化的二元化转换方法减少词汇化同步转录规则的中间项目, 通过实时判断中间项目有效性的RR-CKY算法来避免冗余项目生成。实验证明, 这两种方法能有效减少解码过程中的中间项目, 提高机器翻译解码效率, 在一定程度上提高机器翻译效果。
关键词: 机器翻译; 树转录翻译模型; 句法分析; RR-CKY算法
Decoding Optimization in Tree Transducer based Translation Model
Shi Chongde, Qiao Xiaodong, Wang Huilin
Institute of Scientific & Technical Information of China, Beijing 100038, China
Abstract
This paper proposes two methods to improve the efficiency of rule binarization and decoding in tree transducer based translation model. The authors convert synchronous transducer rules to four kinds of binary rules to reduce the temporary items, and propose RR-CKY decoding algorithm, which can avoid part of redundant items along with decoding. The experiments show that these two methods can reduce the number of temporary items and make decoding faster. They can also improve the quality of machine translation.
Keyword: Machine translation; Tree transducer based translation model; Parsing; RR-CKY algorithm
1 引 言

近年来, 统计机器翻译的研究重点逐渐从基于短语的翻译模型转向基于句法的翻译模型, 研究者设计开发了多种基于句法的翻译模型[ 1, 2, 3, 4, 5], 基于句法的翻译模型已经成为目前主流的机器翻译模型。

基于句法的翻译模型解码算法大多基于传统的句法分析算法, 在翻译过程中由于翻译规则的复杂性, 以及语言模型嵌入等对解码效率要求比较高, 本文基于树转录翻译模型[ 3], 研究翻译解码的优化算法。

2 国内外研究现状

基于句法的统计机器翻译模型中, 解码主要涉及树结构的分析, 因此大多基于句法分析算法。句法分析相关的研究历史悠久, 成熟的算法包括Chart算法、GLR算法、CKY算法等[ 6]。在早期句法分析中, 由于人工编写的句法规则生成能力过强、句法歧义多, 导致实用性不强。

在统计机器翻译中, CKY算法流程简洁明了、易于实现, 成为绝大多数翻译解码算法的核心算法。但由于机
器翻译涉及到两种语言的规则, 规则一般较长, 部分包含词汇化规则, 因此首先需要将规则转换为乔姆斯基范式 (Chomsky Normal Form, CNF) , 即同步二元化转换 (Synchronous Binarization) , 其转换方法对句法分析的效率影响较大, 同时也关系到是否能实时嵌入语言模型的计算。Zhang等[ 7]研究了同步二元化方法和“串-树”转录规则的二元化问题, 使规则的两种语言可以同时实现二元化, 并实时嵌入语言模型;Wang等[ 8]研究了使用EM算法来确定规则的二元化中使用左二元化还是右二元化, 提高了机器翻译效果。Fang等[ 9]主要通过提前匹配源语言端的词汇和提前嵌入语言模型计算来提高解码效率。

在传统的句法分析研究领域, 随着树库[ 10]资源的兴起和基于机器学习的句法分析模型的出现[ 11, 12, 13], 提高句法分析的效率重新成为研究重点之一。Song等[ 14]认为影响句法分析算法效率的一个重要因素是二元化 (Binarization) 过程中中间项目的数量, 其通过在训练语料上训练一个基于中间项目有效性的排序来确定分析过程中选择哪些中间项目。Schmid[ 15]设计了一种贪婪算法, 通过选择规则右部可能性最高的组合来精简语法规模, 提高算法效率。

本文同样通过减少中间项目数量来提高算法效率, 算法不需要提前训练, 在解码过程中实时监测中间项目的有效性, 通过减少无效项目生成来提高效率。

3 树转录翻译模型

在对不同语言句法结构差异性的研究中发现, 使用传统的短语结构语法 (CFG) 表示句法结构的变换存在很多不足。Fox[ 16]对英语和法语句法成分之间的调序所造成的短语成分交叉进行了深入研究, 发现两种语言的成分结构变换主要与动词短语相关, 因此提出了动词短语扁平化的方法。

图1 “串-树”对齐

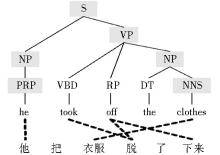
Galley等[ 17]、Graehl等[ 18]基于这种思想提出了树转录翻译模型。以汉英机器翻译为例, 翻译模型首先在训练语料上进行词对齐训练, 并对英语进行句法分析, 将图1的“串-树”对齐转换成如表1所示的同步转录规则, 并通过机器学习算法计算规则翻译概率;解码过程中对源语言端进行句法分析, 同步生成目标语言。

表1 同步转录规则
.
4 四分化规则转换

从同步转录规则抽取需要经过一系列的树结构扁平化操作, 规则右部包含较多词汇和句法范畴, 使用CKY算法首先需要进行二元化转换, 比如规则“S→NP 把 VP”可以转换为“NT1→NP 把”和“S→NT1 VP”两个规则, 常用方法包括左二元化、右二元化等。

在Zhang等[ 7]的研究基础上, 本文定义了4种形式的转换规则, 称为四分化转换, 在实现转录规则的同步二元化的同时, 减少中间项目生成。4种类型的规则定义如下:

(1) 词汇化规则:规则右部汉语、英语均包含 1 个或多个词汇, 不包含句法范畴;

(2) 一元规则:规则右部汉语部分只有 2 个句法范畴, 不包含词汇;英语部分只包含1 个句法范畴和任意个词汇;

(3) 二元规则:规则右部汉语部分只有 2 个句法范畴, 不包含词汇;英语部分只包含2 个句法范畴和任意个词汇;

(4) 混合规则:规则右部汉语部分包含 1 个或者 2 个句法范畴, 任意个词汇;英语部分相同。

这样的转换规则可以保证混合规则只有4种形式, 假设w表示一或多个词汇, N表示句法范畴, 混合规则的4种形式为:wN、Nw、w1Nw2、N1wN2。

四分化转换方法保证了转换后的规则中最多包含2个句法范畴, 使之适用于 CKY算法;同时算法保证了同步嵌入语言模型计算, 假设规则右部只有1个句法范畴的则其先天满足语言模型计算, 假设转换后规则包含2个句法范畴, 可以确定无论是规则的汉语部分还是英语部分, 其词汇句法范畴必然是连续的, 可以进行语言模型计算;词汇化规则、混合规则包含大量词汇, 长度往往大于2, 在一定程度上减少了中间项目数量。

5 RR-CKY解码算法

本文的翻译解码算法基于传统的CKY算法, 通过减少中间项目的生成、避免冗余的规则搜索来提高解码算法的效率, 称之为减冗余CKY算法 (Reduce Redundancy CKY, RR-CKY) 。

5.1 CKY解码算法

本文将解码过程看作一个演绎证明系统[ 2, 19], 系统用一系列带权重的项目 (Items) 来表示句法分析过程的状态, 形式如下:
I1:w1…Ik:wkI:wΦ

表示如果分子部分的Ii可证明 (权重为wi) , 则I可证明 (权重为w) 。句法分析的过程转换为一个从公理 (Axioms) 开始, 逐步套用规则推导到最终目标的过程。CKY算法中项目有两种形式:

(1) [X, i, j], 表示在句子跨度为i, j的区间上可以推理识别X这个项目;

(2) (X→γ) , 表示语法中的规则。

推导过程主要包括两种规则:

①Z→fi+1:w[Z, i, i+1]:w

②Z→XY:w[X, i, k]:w1[Y, k, j]:w2[Z, i, j]:ww1w2

其中, 前者表示规则右部只有一个项目的推理规则, 后者表示右部含有两个项目的推理规则, w表示规则概率。

翻译解码首先将训练得到的规则转换为上文的4种形式, 利用规则的汉语部分进行CKY解码, 同时生成英语。CKY解码核心流程如下所示:

①w0, w1, …, wL←read_sentence ()

②mark_mrule_position ()

③apply_lexical_rule ()

④for l∈ (2, L) do

⑤for s∈ (0, L－l) do

⑥for t∈ (1, l－1) do

⑦apply_binary_rule (s, s+t, s+l)

⑧apply_mixed_rule (s, s+l)

⑨apply_unary_rule (s, s+l)

⑩sort_and_prune (s, s+l)

B11output_english_sentence ()

算法中步骤①读入长度为L的汉语句;步骤②预处理主要通过混合规则中的词汇来标记其可能需要应用的位置;步骤③对汉语句子应用词汇规则生成一部分项目, 这同时包括应用一或多个汉语词的规则;步骤④-⑥为CKY算法循环;步骤⑦在循环内部应用二元化规则, 尝试从跨度 (s, t) 和 (t, l) 上生成 (s, l) 上的新的项目;步骤⑧尝试在跨度 (s, l) 上应用混合规则生成新的项目;步骤⑨尝试使用一元规则生成新的项目, 为了防止陷入死循环, 所有现有的项目只应用一次一元规则;步骤⑩计算规约后短语的评分, 并对所有规约生成的项目进行排序, 如果需要则进行剪枝。在整个循环结束之后, 步骤B11检查跨度为 (0, L) 的项目中是否包含标记为“S”、“ROOT”等的项目, 如果存在则输出分值最高的1或n个翻译结果。

CKY算法本身是一种高效的解码算法, 复杂度为O (n3) , 但是在树转录语法的解码中, 由于规则的长度比较长, 二元转换时产生的中间项目较多, 算法复杂度要远大于O (n3) 。从解码算法可以看出, 步骤⑦应用二元规则中需要分别从跨度 (s, s+t) 和 (s+t, s+l) 中选择两个项目NT1和NT2, 并搜索二元规则库中是否含有相关规则, 因此这两个跨度所包含的项目的数量同样会影响整个算法的效率。

实际上, 在不同语法规模下, 随着每个跨度长度的增加, 其包含的中间项目的数量也急剧增加, 甚至达到句子长度n的上万倍, 在嵌入语言模型的情况下, 算法复杂度为:O (n3 (|NT|·|T|2 (m－1))K) , 其中|NT|表示项目数, T表示词汇数, m表示语法模型元数, K表示规则右部最大长度[ 20]。这种情况下, 提高算法效率的一个有效方法是减少中间项目的数量, 即NT中的项目数。

5.2 冗余项目定义

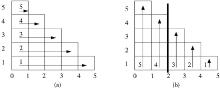
CKY算法的循环顺序见图2 (a) 。其中, 横轴表示对应的句中的词的起始点, 纵轴表示生成项目的跨度大小, 箭头及其标号表示生成的顺序和方向。因此, 传统的CKY算法生成从左至右, 项目的跨度从小到大, 首先生成 (0, 1) , (1, 2) , …跨度为1的项目, 然后生成 (0, 2) , (1, 3) , …跨度为2的项目, 直到最终生成目标项目 (0, 5) 。也就是说, 为了从 (i, k) 和 (k, j) 跨度生成 (i, j) 跨度的项目, 首先必然会在 (i, k) 和 (k, j) 中生成所有可能的中间项目。

但实际上, 跨度 (i, k) 中的某个中间项目NT1可能无法在跨度 (k, j) 中找到相应的项目进行组合, 以适用于某一规则生成新的项目, 本文把这种类型的中间项目称为冗余项目, 通过减少冗余项目, 可以在一定程度上提高解码算法的效率。

定义:假设有规则A→B C, 如果B同时满足下列三个约束条件:

(1) 在生成项目 (i, k, B) 时明确知道后续所有跨度 (k, j1) , (k, j2) , …中均不可能产生项目C;

(2) 一元规则中不存在这样的规则X→B;

(3) 二元规则和混合规则中不存在这样的规则:X→Y1Y2…B, 即B不能作为规则右部最后一个项目。

这样的项目 (i, k, B) 称为冗余项目。

冗余项目 (i, k, B) 将不被放入 (i, k) 跨度的项目集合, 在后续利用 (i, k) 跨度的项目生成更大跨度项目的时候就避免了包含冗余项目规则的匹配。本文把这种算法称为减冗余CKY算法。

5.3 冗余项目识别与解码优化

基于对冗余项目的减除, 对CKY算法进行了优化。优化算法实现主要分两步:

(1) 在解码器读入树转录规则并转换为4种转换规则之后, 建立两个数据结构:nt_in_tail, suffix_map, 其中前者是一个列表, 表示在一元规则、二元规则和混合规则中的最靠右的一个项目;后者是一个“键-值”对, “键”表示任意一个项目B, 对应的“值”是B的后缀列表, 即所有二元规则、混合规则中B的后一个词汇或句法范畴的列表。

(2) 对CKY算法进行调整。其中最重要的一点是调整CKY算法的外循环顺序, 传统CKY算法的项目生成顺序是从左至右、从下至上, 逐步生成跨度更大的项目, 如图2 (a) , 无法对上述第一个约束条件进行判断。本文将循环顺序改为从右至左, 自下而上进行生成, 逐步生成左边界更小的项目, 如图2 (b) 的生成顺序为: (4, 5) | (3, 4) , (3, 5) | (2, 3) , (2, 4) , (2, 5) | (1, 2) , (1, 3) , (1, 4) , (1, 5) | (0, 1) , (0, 2) , (0, 3) , (0, 4) , (0, 5) , 这样可以保证在生成 (0, 2) , (1, 2) 等以图中粗线条为右边界的项目时, 所有以粗线条为左边界的项目均已生成, 以使用上述第一个约束条件排除冗余。

图2 CKY算法循环方向

上述例子描述的RR-CKY算法循环顺序为从右至左 (RL-RR-CKY) , 同理也有从左至右RR-CKY算法 (LR-RR-CKY) 循环, 两种不同方向的RR-CKY算法循环及主要步骤如下, 其他步骤与CKY解码核心流程完全相同。

RL-RR-CKY算法:

④for s∈ (L－2, 0) do

⑤for l∈ (s+2, L) do

⑥for t∈ (s+1, l－1) do

⑦apply_binary_rule (s, t, l)

⑧apply_mixed_rule (s, l)

⑨apply_unary_rule (s, l)

⑩sort_and_prune (s, l)

LR-RR-CKY算法:

④for l∈ (2, L) do

⑤for s∈ (l－2, 0) do

⑥for t∈ (s+1, l－1) do

⑦apply_binary_rule (s, t, l)

⑧apply_mixed_rule (s, l)

⑨apply_unary_rule (s, l)

⑩sort_and_prune (s, l)

与传统CKY算法不同之处在于, 使用两种不同方向的RR-CKY算法步骤⑦-⑩的每一类规则新生成项目的时候, 均需要判断新项目是否冗余, 然后决定是否将新项目添加到对应跨度的项目列表中, 判断中间项目是否冗余的算法如下:

①if j == L

②return False

③else if new_nt ∈ nt_in_tail

④return False

⑤else if suffix_map[new_nt]∩nts[j] == Φ

⑥return True

以从右到左的RR-CKY算法为例, 判断新生成项目是否冗余的核心是判断新项目的后缀表与右部现有的项目是否有交集, 如果没有则判断新项目为冗余, 从而避免在后一步分析过程中进行多余的规则搜索操作。

6 实验结果与分析

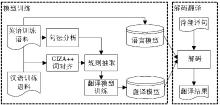
为验证算法的有效性, 进行了汉英机器翻译实验。翻译训练语料为LDC汉英双语语料约20万句, 使用GIZA++[ 21]进行词对齐, 英语部分使用斯坦福句法分析器[ 22]进行句法分析, 并用SRILM[ 23]进行训练得到语言模型。实验系统包含翻译模型和语言模型, 翻译系统架构如图3所示:

图3 翻译系统架构

6.1 规则转换实验

本实验主要对左二元化和四分化转换的规则数量和效率进行对比。简化起见, 仅使用翻译模型, 不嵌入语言模型, 不使用剪枝策略。在不进行任何剪枝的情况下, 为了防止翻译候选的组合爆炸, 选择测试语料为长度小于20的测试句共20句进行。

在载入规则过程中, 限定其项目数在5个以下, 总长度在10个以下, 同时过滤掉含有输入文本所包含词汇以外词汇的规则。实验结果如表2所示。

为了便于比较, 表2中将左二元化方法转换后得到的规则按照四分化的4种类型进行分类统计。从两者对比可以看出, 四分化转换方法生成的中间项目约为左二元化方法的一半, 解码时间也大大缩短。

表2 规则转换实验对比

另外, 由于同步多元规则本身的特性, 部分规则无法按照相邻和连续的原则进行转换, 占比约0.8%, 不过在大规模训练语料上基本可以忽略这一影响。

6.2 RR-CKY解码效率对比实验

本实验主要验证RR-CKY算法能在多大程度上减少中间项目的生成。实验各项设定与规则转换实验相同。

实验分别对传统CKY算法、LR-RR-CKY算法及RL-RR-CKY算法的解码结果和解码效率进行对比。实验结果如表3所示:

表3 解码算法效率对比

从表3可以看出, RR-CKY算法比传统的CKY算法生成的中间项目数更少, 效率更高, 从右向左的算法效率最高, 这主要是由于规则转换过程中的结合顺序。假设原始规则为A → B C D, 规则转换按照左结合进行, 二元化之后为:NT1→B C;A→NT1 D。假设解码过程中遇到“B C E”, 对LR-RR-CKY算法来说, 首先会生成NT1, 下一步发现“NT1 E”无法继续, NT1就是一个无效项目;而对RL-RR-CKY算法来说, 在准备生成NT1项目的时候需观察右部是否已经有D项目, 有则生成、无则放弃, 在这种情况下NT1被直接抛弃, 下一步就不需要查询是否有右部为“NT1 E”的规则, 提高了算法效率。

6.3 翻译效果对比实验

本实验主要为观察优化算法对机器翻译效果的影响, 使用NIST[ 24]2002年测试语料作为开发集, 2003年的测试语料作为测试集, 翻译模型与语言模型的权重通过MERT[ 25]进行优化。实验嵌入了语言模型, 并使用剪枝策略, 每一步规约保留评分靠前的50个翻译。最终翻译使用BLEU评分效果如表4所示:

表4 翻译评分

传统CKY解码过程中可能对一些无效项目评分较高, 在剪枝过程中可能会被保留, 从而对最终翻译结果产生不好的影响, 而使用RR-CKY能避免一部分这种情况, 因此翻译效果更好一些。

7 结 语

基于句法的统计机器翻译模型的一个主要瓶颈在于解码时的句法分析效率, 本文针对这一问题提出了四分化的规则二元化方法, 以及RR-CKY算法, 一定程度上减少了解码过程中的临时结点, 提高了算法效率。同时, 本算法也适用于基于CKY算法的句法分析。

目前本文研究的系统还处于试验阶段, 仅包含了翻译模型和语言模型, 在后续的工作中计划加入其他模型, 以提高系统的翻译效果, 同时继续研究和提高算法效率, 以适应更大规模的训练语料和翻译应用。

参考文献
[1] Wu D. Toward Machine Translation with Statistics and Syntax and Semantics[C]. In: Proceedings of the IEEE Workshop on Automatic Speech Recognition and Understand ing (ASRU’09), Merano, Italy. 2009: 12-21. [本文引用:1]
[2] Chiang D. Hierarchical Phrase-based Translation[J]. Computational Linguistics, 2007, 33 (2) : 201-228. [本文引用:2] [JCR: 0.94]
[3] Marcu D, Wang W, Echihabi A, et al. SPMT: Statistical Machine Translation with Syntactified Target Language Phrases[C]. In: Proceedings of the 2006 Conference on Empirical Methods in Natural Language Processing, Sydney, Australia. 2006: 44-52. [本文引用:2]
[4] 刘洋. 树到串统计翻译模型研究[D]. 北京: 中国科学院计算技术研究所, 2007. (Liu Yang. Research on Tree-to-String Statistical Translation Models[D]. Beijing: Institute of Computing Technology, Chinese Academy of Sciences, 2007. ) [本文引用:1]
[5] 蒋宏飞. 基于同步树替换文法的统计机器翻译方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2010. (Jiang Hongfei. Research on Synchronous Tree Substitution Grammar Based Statistical Machine Translation Methods[D]. Harbin: Harbin Institute of Technology, 2010. ) [本文引用:1] [CJCR: 0.3432]
[6] 宗成庆. 统计自然语言处理[M]. 北京: 清华大学出版社, 2008. (Zong Chengqing. Statistical Natural Language Processing[M]. Beijing: Tsinghua University Press, 2008. ) [本文引用:1]
[7] Zhang H, Huang L, Gildea D, et al. Synchronous Binarization for Machine Translation[C]. In: Proceedings of the Human Language Technology Conference of the North American Chapter of the Association of Computational Linguistics. Stroudsburg, PA, USA: Association for Computational Linguistics, 2006: 256-263. [本文引用:2]
[8] Wang W, Knight K, Marcu D. Binarizing Syntax Trees to Improve Syntax-based Machine Translation Accuracy[C]. In: Proceedings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, Prague, Czech Republic. Stroudsburg, PA, USA: Association for Computational Linguistics, 2007: 746-754. [本文引用:1]
[9] Fang L, Chung T, Gildea D. Terminal-aware Synchronous Binarization[C]. In: Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics, Portland , Oregon, USA. 2011: 401-406. [本文引用:1]
[10] The Penn Treebank Project[DB/OL]. [2013-06-15]. http://www.cis.upenn.edu/~treebank/. [本文引用:1]
[11] Collins M. Head-driven Statistical Models for Natural Language Parsing[D]. Philadelphia: University of Pennsylvania, 1999. [本文引用:1]
[12] Charniak E. A Maximum-Entropy-Inspired Parser[C]. In: Proceedings of the 1st North American Chapter of the Association for Computational Linguistics Conference. 2000: 132-139. [本文引用:1]
[13] Klein D, Manning C D. Accurate Unlexicalized Parsing[C]. In: Proceedings of the 41st Annual Meeting on Association for Computational Linguistics. 2003: 423-430. [本文引用:1]
[14] Song X, Ding S, Lin C Y. Better Binarization for the CKY Parsing[C]. In: Proceedings of the Conference on Empirical Methods in Natural Language Processing, Honolulu, Hawaii, USA. 2008: 167-176. [本文引用:1]
[15] Schmid H. Efficient Parsing of Highly Ambiguous Context-free Grammars with Bit Vectors[C]. In: Proceedings of the 20th International Conference on Computational Linguistics. 2004. [本文引用:1]
[16] Fox H J. Phrasal Cohesion and Statistical Machine Translation[C]. In: Proceedings of the ACL-02 Conference on Empirical Methods in Natural Language Processing. Stroudsburg, PA, USA: Association for Computational Linguistics, 2002: 304-311. [本文引用:1]
[17] Galley M, Hopkins M, Knight K, et al. What’s in a Translation Rule?[C]. In: Proceedings of the Human Language Technology and North American Association for Computational Linguistics Conference (HLT-NAACL 2004), Boston, Massachusetts, USA. 2004: 273-280. [本文引用:1]
[18] Graehl J, Knight K, May J. Training Tree Transducers[J]. Computational Linguistics, 2008, 34 (3) : 391-427. [本文引用:1] [JCR: 0.94]
[19] Goodman J. Semiring Parsing[J]. Computational Linguistics, 1999, 25 (4) : 573-605. [本文引用:1] [JCR: 0.94]
[20] Venugopal A, Zollmann A, Vogel S. An Efficient Two-Pass Approach to Synchronous-CFG Driven Statistical MT[C]. In: Proceedings of Human Language Technology and North American Association for Computational Linguistics Conference, Rocherster, NY, USA. 2007: 500-507. [本文引用:1]
[21] GIZA++[CP/OL]. [2013-06-15]. http://code.google.com/p/giza-pp/. [本文引用:1]
[22] The Stanford Parser[CP/OL]. [2013-06-15]. http://nlp.stanford.edu/software/lex-parser.shtml. [本文引用:1]
[23] SRILM[CP/OL]. [2013-06-15]. http://www.speech.sri.com/projects/srilm/. [本文引用:1]
[24] NIST Open Machine Translation (OpenMT) Evaluation[DB/OL]. [2013-06-15]. http://www.itl.nist.gov/iad/mig//tests/mt/. [本文引用:1]
[25] Och F J. Minimum Error Rate Training in Statistical Machine Translation[C]. In: Proceedings of the 41st Annual meeting on Association for Computational Linguistics, Sapporo, Japan. Stroudsburg, PA, USA: Association for Computational Linguistics, 2003: 160-167. [本文引用:1]