引用本文
赵辉, 刘怀亮. 面向用户生成内容的短文本聚类算法研究. 现代图书情报技术,
Zhao Hui, Liu Huailiang. Research on Short Text Clustering Algorithm for User Generated Content. New Technology of Library and Information Service,   
Permissions
面向用户生成内容的短文本聚类算法研究
赵辉, 刘怀亮
西安电子科技大学经济与管理学院 西安 710071
摘要
关键词: 短文本聚类; 特征扩展; 复杂网络; K-means算法; 用户生成内容
Research on Short Text Clustering Algorithm for User Generated Content
Zhao Hui, Liu Huailiang
School of Economics & Management, Xidian University, Xi’an 710071, China
Abstract
To solve the problem of weak semantic description ability of short text feature in user generated content, and the traditional K-means algorithm for document clustering is sensitive to the initial clustering center, this paper proposes that the semantic features information of short text can be supplied by feature extension based on the concept, link structure and category system of Wikipedia. Then the weighted complex network of short text set is built by the semantic relation of texts, and text clustering is achieved by node partitioning community based on K-means algorithm whose initial clustering center is chosen according to the synthetic characteristics of network nodes. Results of experiment show that the algorithm proposed by this paper can improve the effect of short text clustering.
Keyword: Short text clustering; Feature extension; Complex network; K-means algorithm; User generated content
1 引 言

用户生成内容 (User Generated Content, UGC) 是指用户自身在互联网上创作和发表的文字、图片、音频等内容, 作为一种新兴的网络信息创作与组织模式, 它通常由微博、社交网站 (SNS) 、在线问答等社会化媒体发布[ 1], 形式上主要以即时消息、问题、评论等非结构化短文本数据为主。随着互联网中这些短文本数据的爆炸式增长, 人们迫切需要对这些用户生成内容进行聚类处理以便快速获取有用的信息。

聚类分析作为一种重要的知识发现手段, 是指将对象按其特性的相似程度进行归类的过程。在传统的基于向量空间模型的文本聚类过程中, 文本间相似度受词重叠数目影响较大, 而短文本与长文本相比, 一般含有的特征词较少, 易造成描述概念信号弱、噪音数据多及特征稀疏性明显等问题[ 2], 因而影响了文本相似度计算的效果。此外, 在文本聚类中得到广泛应用的K-means聚类算法[ 3]虽具有计算简单且收敛速度快的优点, 但也存在着对初始聚类中心选值的敏感性问题、容易陷入局部极值等问题[ 4]。上述问题使得传统的K-means聚类算法对于短文本不能取得令人满意的效果。
为解决短文本特征少且描述信息弱的问题, 近年来有学者开始利用外部信息对短文本进行特征扩展以辅助文本表示, 该研究主要集中在短文本分类领域, 如宁亚辉等[ 5]、王盛等[ 6]利用知网对短文本进行特征扩展, 但是语义词典的可扩展性差且更新速度慢, 难以满足用户生成内容中短文本处理的需求。范云杰等[ 7]利用维基百科对短文本进行特征扩展, 其采用考虑概念类别因素基于tf-idf法计算概念间相关度。在短文本聚类领域, 白秋产等[ 8]通过结合HowNet的概念属性进行特征扩展以提高文本聚类效果。

此外, 随着小世界特性在语言复杂网络中的发现, 一些学者开始研究利用复杂网络节点特性来解决K-means算法对初始聚类中心选择的敏感性问题。如Pan等[ 9]通过节点度来选取初始聚类中心以改善K-means聚类算法的性能。赵鹏等[ 10]、董俊等[ 11]综合考虑网络中的节点度与聚集系数进行初始聚类中心的选择。文献[12]通过综合考虑节点加权度、加权聚集系数与节点介数进行节点特性计算, 并以此为基础进行文本特征选择, 实验中取得了较好的效果, 这为初始聚类中心选取提供了新的方法。

本文研究并提出一种基于维基百科的特征扩展方法并将其应用于基于复杂网络的K-means短文本聚类算法:通过外部知识源维基百科对短文本进行扩展以丰富短文本的语义表达能力, 与文献[7]有所不同, 本文利用链接结构和类别体系信息进行概念间相关度计算; 以文本间语义相似度为基础构建文本集加权复杂网络, 通过文献[12]的节点综合特性度量方法选取能够代表文本类别语义特征的关键节点作为初始聚类中心; 利用K-means聚类算法对复杂网络节点进行社团划分以形成聚类, 从而完成对语义相近文本的聚类, 以此达到提高短文本聚类效果的目的。

2 基于复杂网络的短文本聚类算法研究
2.1 基本思想

为提高短文本特征描述能力, 本文首先提出基于维基百科的特征扩展方法对文本特征进行扩展以增强其语义表达能力, 减少向量空间文本表示模型中语义信息的缺失。然后通过建立以文本为节点, 以文本间语义关系为边, 以其语义关系强弱作为边权重的文本集加权复杂网络来表示文本间的语义关系, 以此为基础通过节点综合特性全面衡量节点所对应文本在其所属类别的语义代表性, 进而进行初始聚类中心的选取, 以此解决K-means聚类算法对初始化选值敏感性的问题。最后结合K-means算法对网络节点进行社团划分, 以完成对节点所对应短文本聚类的目的。

2.2 基于维基百科的特征扩展方法

由于互联网中UGC短文含有较多的缩写词、俗语、流行语、专业术语等词语, 普通的语义词典难以识别, 而维基百科作为一个以开放和用户协作编辑为特点的Web2.0知识系统, 具有知识覆盖面广、结构化程度高、信息更新速度快等优点[ 12]。所以本文以维基百科知识库为数据源, 利用其所蕴含的概念、重定向及其链接等信息对短文本进行特征扩展:将特征词转化为主题概念; 对主题概念进行相关概念的抽取; 对所抽取的主题概念与相关概念间的相关关系进行量化, 进而根据需要对相关概念进行筛选以完成短文本的特征扩展。特征扩展的具体过程如下:

(1) 将特征词tk映射为维基百科中存在的主题概念Ck。当该特征词存在重定向时, 以重定向的概念作为特征词tk的主题概念。

(2) 利用维基百科网页间链接关系从维基百科中抽取相关概念。由于页面上的部分锚文本所对应的概念与主题概念相关性不强, 为去除这种弱相关关系词, 只选取与主题概念Ck具有互相链接关系的概念作为相关概念。由此, 可以得到主题概念Ck相关的概念集合Ck (C1, C2, …, Cn) , 其中Ck与Ci (1≤i≤n) 间具有相互链接关系。

(3) 语义相关关系量化是为了区分相关概念集合中不同概念对主题概念的贡献度, 本文主要运用维基百科的链接结构和类别体系分别计算概念间的链接距离和类别距离, 然后将这两者进行线性组合计算概念间的相关度。

①链接距离

采用WLM法[ 13]计算概念Ck、Ci间的链接距离Dlink。
Dlink=log (max (A, B) ) －log (A∩B) log (W) －log (min (A, B) ) (1)

其中, Dlink是指概念Ck、Ci间的链接距离, A、B是指在维基百科中分别与概念Ck、Ci有相互链接关系的概念集合, W则指维基百科中所有概念解释页面的集合。符号“| |”表示取集合中的实体数量。

②类别距离

为减少维基百科主题页面间的链接稀疏性对相关度计算的影响, 本文在链接距离的基础上, 通过计算概念所属类别间的距离, 以便更准确衡量概念间的相关度。

在维基百科的类别体系中, 虽然节点间路径可能不唯一, 但其中必然存在一条最短路径d, 而两节点间的最短路径越小, 则其距离就越近, 那么类别间的相关程度也就越高。此外, 由于概念可能属于多个类别, 那么两个概念间就可能存在多种分类关系的组合, 也就可能对应存在多个最短路径。本文将其中最小的最短路径值作为两概念之间的类别距离, 则概念Ck与Ci之间的类别距离计算公式定义为:
Dcat (Ck, Ci) =log (min (dki) +1) (2)

其中, dki表示概念Ck、Ci所属类别之间的最短路径距离, 取log值是为了使dki变化幅度平均化, 抑制类别距离与链接距离之间过大的差异。

③相关度计算方法

为了较全面地衡量概念间的相关度, 概念间语义距离应该综合考虑维基百科链接结构和类别体系中蕴含的概念间关系。本文定义的主题概念Ck与其相关概念Ci间的概念语义距离计算公式如下所示, 形式上表现为链接距离Dlink和类别距离Dcat的线性组合:

D (Ck, Ci) =αDlink (Ck, Ci) + (1－α) DcatCk, Ci (3)

其中, α (0≤α≤1) 为调节参数。由于概念与其本身的距离为0, 相关度设为1, 随着距离的增大, 概念间的相关关系越小, 当语义距离趋于无穷大时, 相关度为0。因此, 本文将概念间的相关度计算公式定义为:
RCk, Ci=1D (Ck, Ci) +1 (4)

通过上述过程, 对特征词tk所对应的主题概念Ck构建的相关概念集合为 ( (C1, R1) , (C2, R2) , …, (Cn, Rn) ) , 其中, Ri (1≤i≤n) 表示由公式 (4) 求得的相关概念与主题概念间的相关度。

(4) 通过设定阈值, 从相关概念集合中选取满足条件的概念以完成特征词的扩展。

2.3 基于复杂网络的K-means短文本聚类算法

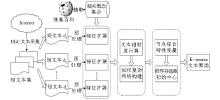
首先将本文提出的基于维基百科的特征扩展方法应用于短文本的表示中; 然后利用复杂网络对经过特征扩展后的短文本集基于语义关联进行组织, 以形成文本集加权复杂网络; 进而对文本网络进行节点综合特性度量, 以寻找能够代表各文本类别语义特征的关键节点作为初始聚类中心; 最后结合K-means算法对节点进行社团划分以实现对语义相近文本的聚类。

基于复杂网络的K-means短文本聚类算法流程如图1所示:

图1 基于复杂网络的K-means短文本聚类算法流程

该流程的具体算法描述如下:

输入:短文本集D

输出:短文本聚类结果

①对短文本集D中每篇文档di进行分词、去停用词。预处理后得到文本的原始特征集合。

②遍历文本原始特征集合中的特征词ti, 若能匹配到维基百科中所对应的概念, 则利用2.2节中的方法对其进行特征扩展, 若匹配失败, 则不进行扩展。扩展完后进行特征权重计算, 然后合并相同特征项, 相应权重进行相加, 其中特征词权重的计算分两种情况:如果是原文档本身存在的特征词, 则其权重由tf-idf[ 14]计算求得; 而扩展得来的词的权重由文献[7]提出的方法求得。

③将短文本集D转化为短文本集加权复杂网络G= (V, E, W) 的形式。其中, V表示网络节点集合, 集合中每个节点表示扩展后的每篇短文本; E 表示连接边eij的集合, 该集合中连接边表示文本间的语义关系; W表示边eij权重的集合。

为了使边eij的权重能够衡量文本间语义关系的强弱, 本文将边的权重定义为文本间的语义相似度, 并采用余弦系数法[ 15]进行计算。此外本文只将文本间相似度大于阈值的文本连接起来。如果不进行阈值控制, 那么将得到近似全连接的网络, 这样会造成大量弱连接的存在, 影响了节点聚类的效率和效果。因此控制阈值对文本进行连接不仅可以控制网络的复杂性, 同时也可以提高复杂网络节点聚类的质量。

④利用文献[12]的方法分别计算复杂网络中节点的综合特征值, 然后将节点按照其综合特性值进行排序, 以形成节点序列Q。

⑤从队列Q中最大的综合特征值节点开始, 依次选取K个与已被选作初始聚类中心节点间无连接边的节点作为初始聚类中心。

⑥将选出的K个节点作为聚类中心, 采用K-means聚类算法, 根据节点间的相似度进行划分迭代, 形成聚类以完成节点所对应短文本的聚类过程。

3 实验与结果分析

本文进行了如下实验:实验语料来自从新华网、凤凰网、新浪爱问等收集的产生于2012年6月至2013年6月间的用户评论及问题, 其中包含娱乐、文化、教育、体育、财经、科技共6个类别各500篇文本 (每篇字数不超过100字) , 维基百科数据来自维基百科网站下载的zhwiki-2012-05-23中文版XML数据集。从每个类别分别随机选取60、80、100、120、140、160篇文本, 以组成6组不同数量的待聚类文本集, 具体实验过程如下:

(1) 初始聚类中心选择的对比实验

为验证本文所提算法中利用节点综合特性进行初始聚类中心选择的效果, 首先进行不同初始中心选择方法下的短文本聚类效果对比实验, 本次实验共分三组且不进行特征扩展, 统一使用中国科学院计算技术研究所的ICTCLAS进行分词, 在构建文本加权复杂网络时, 相似度阈值取0.2[ 10]。

第一组实验使用传统的K-means短文本聚类方法, 即在聚类过程中随机选取聚类中心进行文本聚类。

第二组实验采用文献[10]的方法, 在初始聚类中心的选择中只考虑节点加权度和加权聚集系数因素。

第三组对本文中将文献[12]的节点综合特性度量方法应用于K-means聚类算法初始聚类中心选择的效果进行实验验证。

使用宏平均F1值[ 16]来评价聚类效果, 实验结果如表1所示:

表1 不同初始中心选取实验结果

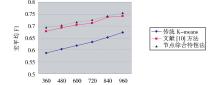
将实验结果绘制成折线图, 如图2所示:

图2 宏平均F1值对比

由表1、图2的实验结果对比可以看出, 利用节点综合特性的方法较传统K-means、文献[10]方法的聚类效果均有所提高。其中与传统K-means相比表明本文所提出的基于复杂网络的短文本聚类算法对解决传统K-means短文本聚类方法对初始聚类中心选值的敏感性问题具有较好的效果; 而与文献[10]方法比较的结果可以看出, 由于综合考虑节点的特性选取初始聚类中心, 聚类中心具有较强的文本类别语义特征代表性和中心性, 因此可以提高K-means算法短文本聚类的准确度。

(2) 短文本特征扩展对聚类效果的影响实验

本实验共分两组, 分别采用特征扩展前后的短文本聚类效果进行对比, 以验证特征扩展对短文本聚类效果的影响, 初始聚类中心选择采用本文的方法。

第一组实验中使用本文所提出的方法进行初始聚类中心选择, 但在聚类过程前对短文本不进行特征扩展处理。第二组实验聚类过程前对短文本使用2.2节中的方法进行特征扩展处理, 经过反复实验, 公式 (3) 中α取0.7, 选取相关度前三位的相关概念集合进行扩展效果较好, 然后再结合复杂网络节点特性进行初始聚类中心选择以进行短文本聚类。扩展前后实验结果如表2所示:

表2 扩展前后实验结果

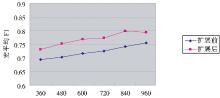
将实验结果绘制成折线图, 如图3所示:

图3 宏平均F1值对比


由表2、图3的实验结果对比可以看出, 扩展后较扩展前的聚类效果均有所提高, 这表明本文所提出的基于维基百科的特征扩展方法可以提高短文本特征的语义表达能力, 以此提高相似度计算的准确度, 从而进一步提高基于K-means算法的短文本聚类的效果。

4 结 语

互联网中社会化媒体的快速发展使得对用户生成内容的处理变得越来越重要, 其中能够处理用户生成的海量短文本信息的聚类技术必然会得到广泛的关注。由于短文本特征较少造成其语义描述能力有限, 加之传统K-means文本聚类算法对初始聚类中心选值的敏感性问题, 使得传统的K-means文本聚类算法对于短文本的聚类效果并不令人满意。因此, 本文提出通过利用维基百科链接、概念和类别体系信息进行特征扩展, 并将其应用于K-means短文本聚类算法, 详细阐述了基于复杂网络的K-means短文本聚类的理论基础和具体实现算法。实验结果表明, 该算法能有效提高短文本聚类的效果。

参考文献
[1] 赵宇翔, 范哲, 朱庆华. 用户生成内容 (UGC) 概念解析及研究进展[J]. 中国图书馆学报, 2012, 38 (5) : 68-81. (Zhao Yuxiang, Fan Zhe, Zhu Qinghua. Conceptualization and Research Progress on User-Generated Content [J]. Journal of Library Science in China, 2012, 38 (5) : 68-81. ) [本文引用:1] [CJCR: 2.697]
[2] 柴春梅. 互联网短文本信息分类关键技术研究[D]. 上海: 上海交通大学, 2009. (Chai Chunmei. The Key Technology Research on Internet Short Text Information Classification[D]. Shanghai: Shanghai Jiaotong University, 2009. ) [本文引用:1]
[3] MacQueen J B. Some Methods for Classification and Analysis of Multivariate Observations[C]. In: Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. 1967: 281-297. [本文引用:1]
[4] 行小帅, 潘进, 焦李成. 基于免疫规划的 K-means 聚类算法[J]. 计算机学报, 2003, 26 (5) : 605-610. (Xing Xiaoshuai, Pan Jin, Jiao Licheng. A Novel K-means Clustering Based on the Immune Programming Algorithm [J]. Chinese Journal of Computers, 2003, 26 (5) : 605-610. ) [本文引用:1] [CJCR: 1.796]
[5] 宁亚辉, 樊兴华, 吴渝. 基于领域词语本体的短文本分类[J]. 计算机科学, 2009, 36 (3) : 142-145. (Ning Yahui, Fan Xinghua, Wu Yu. Short Text Classification Based on Domain Word Ontology[J]. Computer Science, 2009, 36 (3) : 142-145. ) [本文引用:1] [CJCR: 0.61]
[6] 王盛, 樊兴华, 陈现麟. 利用上下位关系的中文短文本分类[J]. 计算机应用, 2010, 30 (3) : 603-611. (Wang Sheng, Fan Xinghua, Chen Xianlin. Chinese Short Text Classification Based on Hyponymy Relation[J]. Journal of Computer Application, 2010, 30 (3) : 603-611. ) [本文引用:1] [CJCR: 0.646]
[7] 范云杰, 刘怀亮. 基于维基百科的中文短文本分类研究[J]. 现代图书情报技术, 2012 (3) : 47-52. (Fan Yunjie, Liu Huailiang. Research on Chinese Short Text Classification Based on Wikipedia[J]. New Technology of Library and Information Service, 2012 (3) : 47-52. ) [本文引用:1] [CJCR: 1.073]
[8] 白秋产, 金春霞. 概念属性扩展的短文本聚类算法[J]. 长春师范学院学报: 自然科学版, 2011, 30 (5) : 29-33. (Bai Qiuchan, Jin Chunxia. Short Text Clustering Algorithm Based on Concept Feature Expansion[J]. Journal of Changchun Normal University: Natural Science, 2011, 30 (5) : 29-33. ) [本文引用:1] [CJCR: 0.2714]
[9] Pan Y, Chen A H, Jiang L L. Improved K-means Clustering Method Based on Complex Network for Rolling Bearing Fault Diagnosis[J]. Applied Mechanics and Materials, 2013, 273: 250-254. [本文引用:1]
[10] 赵鹏, 耿焕同, 蔡庆生, 等. 一种基于加权复杂网络特征的 K-means 聚类算法[J]. 计算机技术与发展, 2007, 17 (9) : 35-37. (Zhao Peng, Geng Huantong, Cai Qingsheng, et al. A Novel K-means Clustering Algorithm Based on Weighted Complex Networks Feature[J]. Computer Technology and Development, 2007, 17 (9) : 35-37. ) [本文引用:2] [CJCR: 0.74]
[11] 董俊, 任家东, 卢海涛. 一种基于复杂网络属性值的 K-means 聚类算法[J]. 燕山大学学报, 2012, 36 (4) : 343-347. (Dong Jun, Ren Jiadong, Lu Haitao. A K-means Cluster Algorithm Based on Complex Networks Attribute Value [J]. Journal of Yanshan University, 2012, 36 (4) : 343-347. ) [本文引用:1] [CJCR: 0.3302]
[12] 赵辉, 刘怀亮, 范云杰. 复杂网络理论在中文文本特征选择中的应用研究[J]. 现代图书情报技术, 2012 (9) : 23-28. (Zhao Hui, Liu Huailiang, Fan Yunjie. Study on the Application of Complex Network Theory in Chinese Text Feature Selection[J]. New Technology of Library and Information Service, 2012 (9) : 23-28. ) [本文引用:1] [CJCR: 1.073]
[13] Milne D, Witten I H. An Effective, Low-cost Measure of Semantic Relatedness Obtained from Wikipedia Links[C]. In: Proceedings of the 1st AAAI Workshop on Wikipedia and Artificial Intelligence. 2008: 25-30. [本文引用:1]
[14] Allen J. Natural Language Understand ing[M]. The Benjamin Cummings Publishing Company, 1991. [本文引用:1] [CJCR: 1.632]
[15] Salton G, McGill M J. Introduction to Modern Information Retrieval[M]. New York, NY, USA: McGraw-Hill, 1983. [本文引用:1]
[16] Sebastiani F. Machine Learning in Automated Text Categorization[J]. ACM Computing Surveys, 2002, 34 (1) : 1-47. [本文引用:1] [JCR: 3.543]