引用本文
原福永, 蔡红蕾. 一种在信任网络中随机游走的推荐算法 . 现代图书情报技术, 2014, 30(10): 70-75
Yuan Fuyong, Cai Honglei. A Recommendation Algorithm Based on Random Walk in Trust Network. New Technology of Library and Information Service, 2014, 30(10): 70-75  
Permissions
Copyright©2014, 《现代图书情报技术》编辑部
《现代图书情报技术》编辑部
一种在信任网络中随机游走的推荐算法
原福永, 蔡红蕾
燕山大学信息科学与工程学院 秦皇岛 066004;河北省计算机虚拟技术与系统集成重点实验室 秦皇岛 066004
通讯作者: 蔡红蕾:E-mail:caihonglei870325@126.com

作者贡献声明：

原福永: 提出研究思路, 设计研究方案;

蔡红蕾: 采集、清洗和分析数据, 进行实验, 论文起草和最终 版本修订。

基金:*本文系国家自然科学基金项目“融合推荐攻击在线集成检测和多维信任机制的可信推荐模型及关键技术研究” (项目编号:61379116)的研究成果之一;
摘要

【目的】 为改善基于信任的推荐算法中显式信任值不够精确、隐式信任值难以度量、信任传播路径不易确定等问题, 提出一种在信任网络中随机游走的推荐算法。【方法】 利用二部图网络结构的一维投影度量用户间的信任值并形成用户间直接信任的矩阵, 把该矩阵作为转移概率矩阵, 用于投影后的用户网中进行带重启动的随机游走, 游走过程直至网络中的信任分布趋于稳定, 即信任熵最大时停止。稳定后的信任分布即为全局信任分布。【结果】 通过在MovieLens数据集上的实验表明, 该算法相比于其他算法, 可以显著提高平均绝对误差(MAE)、平均排序倒数(MRR)、标准化折扣增益值(nDCG)。【局限】 由于二部图网络结构算法固有的冷启动问题, 因此本算法受到新用户/新项目的限制。【结论】 该算法能使推荐更精确并且命中的对象排在列表的前端, 具有很强的应用价值。

关键词: 信任; 二部图网络; 随机游走; 推荐算法
中图分类号:TP301
A Recommendation Algorithm Based on Random Walk in Trust Network
Yuan Fuyong, Cai Honglei
College of Information Science and Engineering, Yanshan University, Qinhuangdao 066004, China;The Key Laboratory for Computer Virtual Technology and System Integration of Hebei Province, Qinhuangdao 066004 ,China
Abstract

[Objective] The current recommendation algorithm based on trust confronted with these issues: the explicit trust value is not accurate enough, the implicit trust value is hard to measure, the trust propagation path is not easy to determine. For that this paper presents a recommendation algorithm based on random walk in the trust network.[Methods] The algorithm uses the Bipartite network-based projection structure measure trust value between users, then these values are the formation of the transition probability matrix for random-walk with restart in the users projection network, random walk process does not stop until the trust distribution tends to be steady, namely the trust maximum entropy is achieved. The trust distribution at this time is the final trust matrix.[Results] The experiments on MovieLens dataset show that the improved Bipartite recommendation algorithm by adding user preferences significantly improves the Mean Absolute Error (MAE), Mean Reciprocal Rank(MRR) and normalize Discounted Cumulative Gain (nDCG) compared to other algorithms.[Limitations] Due to the cold start problems in the Bipartite network-based projection algorithm, this algorithm suffers from the new user/new item problem also.[Conclusions] That is to say, this algorithm can make the recommendation more accurate and successfully recommended objects rank in the front of the list, so this algorithm has a strong application value.

Keyword: Trust; Bipartite network-based; Random-walk; Recommendation algorithm
1 概述

互联网的普及和应用给用户带来信息实时化获取的便捷, 大大地满足用户对各种信息的需求。但同时, 正是这种信息量的快速增长, 使得用户的搜索难以定位。推荐系统能很好地解决信息超载问题并克服搜索引擎结果单一的缺陷。当下个性化推荐主要分为基于内容的推荐、协同过滤推荐、基于二部图网络结构的推荐、基于信任的推荐以及将上述的两种或多种综合起来的混合型推荐。

(1) 基于内容的推荐算法

基于内容的推荐首先分析用户已经选择过的内容, 为用户和对象分别建立、更新其配置文件。然后根据对象(主题、性质、外貌等)的描述与目标用户配置文件中用户偏好的描述进行匹配[ 1], 匹配程度大的对象优先被推荐。基于内容的推荐不存在冷启动问题、数据稀疏性问题。但该算法由于推荐对象“过于”与用户偏好相似[ 2], 导致缺乏多样性, 并且文本特征抽取时受技术限制。

(2) 协同过滤推荐算法

协同过滤推荐是在用户群中找到目标用户的邻居用户, 综合这些用户对指定对象的评价, 预测目标用户对此对象的喜好程度[ 3, 4]。协同过滤推荐算法不受推荐内容形式的制约, 可以处理复杂的非结构化对象[ 5]。但是不足的是, 协同过滤依赖于用户–对象的评分矩阵, 因此受到冷启动[ 6]和数据稀疏性[ 7]问题的限制。

(3) 基于二部图网络结构的推荐算法

基于网络结构的推荐算法不考虑用户和对象的内容形式, 仅仅将其看成抽象的节点, 算法的设计思路只利用用户和对象的选择关系[ 8, 9]。这种算法效果明显好于经典的协同过滤, 但是这类算法依赖于用户–对象的评分矩阵, 因此也受到冷启动和一定程度上的数据稀疏性问题的限制。

(4) 基于信任网络的推荐算法

信任网络模拟现实社会中的人际关系, 用户相比于陌生人更愿意接受其信任的用户给予的推荐[ 10]。该类算法与协同过滤算法相比, 能产生更多可推荐的对象, 可以缓解一定程度上的数据稀疏性问题。但这类算法会因为显式信任值不够个性化、隐式信任值难以确定以及信任值传播时路径和概率的复杂程度导致推荐系统不够精确和稳定。

(5) 混合型推荐算法

混合型推荐算法避免单独使用一种算法时的不足, 一定程度上提高了推荐能力[ 11]。但同时增加了时间和空间的复杂度[ 12, 13]。并且过程中各算法混合的方式和比例不同, 推荐效果大相径庭。因此, 如何使各种推荐算法达到最完美的结合, 并且使最后的混合算法更稳定、精确是该类算法研究的难点与重点。

2 相关工作
2.1 二部图网络结构

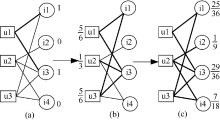
在二部图结构的资源分配[ 8]中, 把用户和对象看作一种抽象的节点。该算法分为两步: 目标用户已经选择的对象把该对象拥有的推荐能力值根据选择关系分配给其他用户; 获得推荐能力值的用户再把值按照选择关系重新分配给对象。上述的简单举例如 图1所示:

图1 简单的二部图资源分配举例

以第一个用户为目标用户, 图1中的粗线代表资源分配的依据。经推算, 两次分配后, 任意对象i从另一任意对象j处获得的推荐资源值如公式(1)所示:

(1)

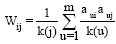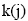
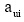
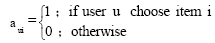其中, 是对象j被选择的次数, 即对象j的度, 是用户u选择对象的总数, 即用户u的度, 其余符号同理。 的定义如公式(2)所示:

(2)

图1中, 用户u1为目标用户时, 对象i1、i3为目标用户选择过的对象, 因此赋予初始值为1, 资源由对象类向用户类分配时, 用户类得到的资源值情况为:

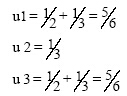
而资源值由用户类向对象类分配时, 对象类得到的资源值情况为:

根据公式(1)可以计算出任意对象i从对象j处获得的资源值, 由此可得出一个n×n的权重矩阵W。根据公式(2)把所有目标用户已经选择过的对象赋予初始值1, 这样所有对象的初始值成为一个0-1的n维向量。把此向量设为f, 用f′表示所有对象最后获取到的资源值向量, 该向量由初始值向量f和由矩阵W相乘所得, 即f′=w×f。对该最终向量f′按照资源值大小降序排列, 取前k个对象形成推荐列表推荐给用户。

2.2 二部图网络结构的一维投影

文献[ 14]实现对二部图网络结构进行一维投影的算法BGPR, 在原来的用户–对象网中, 按照一定规则进行计算, 使其成为一维的用户–用户网或者对象–对象网。本文把两个同类节点在一维网上的边权重定义为共同节点的数目。例如用户x、y, 在二部图网络结构向一维用户网投影时, 两个用户间边权重的定义如公式(3)所示:

(3)

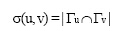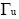
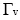
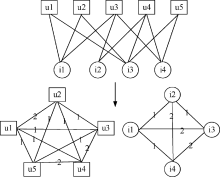
其中, 表示用户u选择的对象集合, 同理。

由文献[ 14]可知, 简单的二部图网络结构向一维网投影过程如 图2所示:

图2 二部图网络结构向一维投影的示例

图2是由一个二部图网络结构投影到用户–用户的一维网(左下)和对象–对象的一维网(右下)的过程。

3 一种在信任网络中随机游走的推荐算法

本文是基于信任的推荐算法受到显式信任值不够精确、隐式信任值难以度量、信任传播路径不易确定等问题的制约下, 提出的一种在信任网络中随机游走的推荐算法RWT。该算法分成4个部分:

(1) 对二部图网络结构进行一维投影, 得到用户–用户间的关系矩阵(直接信任矩阵);

(2) 在用户–用户的一维关系网中随机游走, 步骤(1)得到的关系矩阵式作为随机游走时的转移概率矩阵;

(3) 对随机游走寻求终止条件来结束游走过程, 终止后所有节点的信任分布值即为目标用户对其他用户的全局信任值;

(4) 根据信任用户的信任值及信任用户对指定对象的评分进行推荐。

3.1 用户关系矩阵的获取

在文献[ 8]中, 由公式(1)可得任意节点从其他节点获得的资源值, 该算法利用的只有共同节点之间的数目, 这些关系只源自“度”的关联。在文献[ 14]中, 对二部图网络结构进行一维投影, 计算用户间边权重时只是利用共同选择的对象数目, 见公式(3)。本文对这两种算法进行改进, 把用户j从用户i处获得的资源值定义为用户i对用户j的信任值。并且信任值除了与用户间选择对象的交集大小有关之外, 还与对象的评分有关。

(1) 对对象资源值的初值进行预处理, 按照用户对对象的评分高低对对象资源的初始值进行归一化处理。归一化过程如公式(4)所示:

(4)

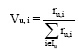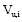
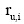
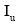
其中, 是以用户u为目标用户时对象i的资源初始值。 是用户u对i的评分, 是用户u的评分对象集合。

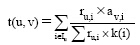(2) 在二部图网络中进行资源从对象类节点向用户类节点的分配, 分配规则是任意对象i分配给相邻用户节点的资源值是 除以该对象i的度; 任意用户v在分配中获得的资源值是所有相邻对象节点分配的资源值总和[ 8]。由此, 任意两个用户u、v经过归一化处理和资源值的分配后, 两个用户之间直接信任值如公式(5)所示:

(5)

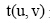
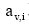
其中, 是用户u对用户v的直接信任值, 取值见公式(2), 是对象i的度。按照公式(5)可得出任意用户间的直接信任值, 由此可得用户间的一个直接信任矩阵S, 该矩阵是3.2节中随机游走时的转移概率矩阵。

3.2 带重启动的随机游走(RWR)

Fouss等[ 15]描述了带重启动的随机游走是图结构中的一种游走形式, 是从图中某个节点出发, 沿着边以一定概率的随机游走。游走过程如公式(6)所示:

(6)

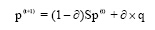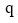
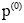
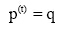
在本文中, 关系转移概率矩阵S即为3.1节中求出的直接信任矩阵S。 是以u为目标用户时, 利用公式(5)得到的对用户的信任向量列。 是初始状态值, 即 。经过实验反复对比,∂取0.8时效果最好(见 图3)。

3.3 随机游走的停止条件

在信息论中, 熵被认定为对不确定性的量度, 熵的定义是: 假设集合S内存在n个元素, S ={E1,···,En}, 每个元素的概率分布为 P={p(E1),···, p(En)}, 则每个元素本身的信息量如公式(7)所示:

(7)

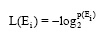而整个信源的信息熵如公式(8)所示:

(8)

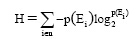熵的性质有: 元素概率分布最均匀, 信息熵最大。在本文中, 用户网中的信息即为信任值, 信源即为目标用户对其他用户的信任分布, 即把上述的信息熵定义为信任熵, 则整个网络的信任熵如公式(9)所示:

(9)

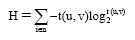对文献[ 14]的随机游走过程进行改进, 处理3.2节中随机游走的迭代时, 在信任熵最大时停止迭代。如公式(10)所示:

(10)

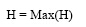在3.2节中随机游走过程的迭代, 每迭代一次, 信任分布较迭代前更均匀, 信任熵越大。迭代停止条件是整个用户网的信任熵H达到最大。在该节中能产生以用户u为目标用户时, 对其他用户的信任列向量T。

3.4 利用信任用户产生推荐列表

由3.3节可得出目标用户的信任用户列表以及对这些用户的信任值。当预测目标用户对指定对象评分时, 由信任列表中的用户对该对象的评分产生预测。预测评分的规则如公式(11)所示:

(11)

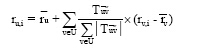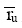
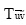
其中, 是目标用户u的评分均值, 是目标用户对信任用户v的最终信任值, U是目标用户的信任用户集合。

3.5 详细步骤说明

输入: 用户–对象的评分矩阵R, 以及目标用户u

输出: 对用户u的推荐列表

(1) 按照3.1节所示对评分矩阵R进行归一化的预处理, 见公式(4), 处理后把资源值由对象类节点向用户类节点分配, 分配原则见公式(5)。

(2) 由步骤(1)获得目标用户u的直接信任用户列表及信任值, 把该列表和值作为初始向量, 按照公式(6)在用户网中进行带重启动的随机游走。

(3) 对随机游走过程进行迭代, 每次迭代计算此时的信任熵, 信任熵达到最大时停止随机游走过程。

(4) 按照步骤(3)得到目标用户对其他用户的最终信任值, 对目标用户未评分的对象进行评分预测, 把预测值按照大小排列, 取前k个形成推荐列表呈现给用户。

4 实验结果及分析
4.1 数据集

实验采用MovieLens站点提供的数据集, 该数据集包括943个用户, 1 682部电影, 10万条评分数据。数据集划分为训练集和测试集, 训练集占80％, 测试集占20%。

4.2 推荐的评价标准

MAP是平均准确率的简称, 是反映系统在全部推荐上性能的单值指标[ 16]。系统推荐成功的项目越靠前(Rank越高), MAP就应该越高。

MRR是平均排序倒数的简称, MRR强调的是第一个命中对象的位置[ 16], 每个用户第一个推荐成功的对象越靠前, MRR应该越高。

DCG是折扣增益值的简称, 其思想是等级高的结果位置越靠前, 则值应该越高[ 16]。DCG的计算方法如下所示:

(12)

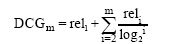为了便于不同结果之间的比较, 可以对 DCG 进行归一, 最常用的计算方法是通过除以每一个排序的理想值IDCG(Ideal DCG)来进行归一。具体如下所示:

(13)

4.3 实验结果及分析

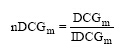(1) 不同参数下的实验对比

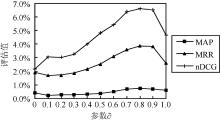
在公式(6)中, 参数∂是重启动因子, 是由节点回到出发点的概率。∂在不同取值下的实验结果如 图3所示:

图3 参数取不同值时实验结果图

由 图3可知参数在取0.8时, 实验效果最佳。因此, 本文与其他算法的对比是在∂=0.8时的实验数据。

(2) 与其他推荐算法的对比

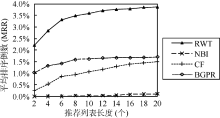
分别与二部图网络结构推荐算法(NBI)[ 8]、经典协同过滤算法(CF)[ 5]、结合二部图投影与排序的协同过滤算法BGPR[ 14]进行对比实验。结果如 图4 – 图6所示:

图4 关于MAP的实验对比图

图5 关于MRR的实验对比图

图6 关于nDCG的实验对比图

由 图4可知, 本文提出的算法能提高系统的MAP值, 即能使推荐系统命中用户喜好的项目, 同时要求命中的项目在推荐列表中的排名靠前。

由 图5可知, 本文提出的算法能提高系统的MRR值, 即能使推荐系统快速地定位用户偏好的对象。

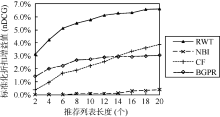
由 图6可知, 本文提出的算法能提高系统的nDCG值, 即能使推荐列表较多地命中对象, 这些对象也正是用户喜好的(评分高的)。

5 结论

本文提出的算法对二部图网络结构进行一维投影, 得到用户–用户间的直接信任矩阵, 并利用该矩阵在用户–用户的一维关系网中随机游走, 在信任熵最大时停止游走过程, 终止后所有节点的信任分布值即为目标用户对其他用户的全局信任值, 利用这些信任用户的信任值及对对象的评分进行评分预测。通过实验表明本算法能使用户在最少的浏览下定位到自己喜好的对象, 具有很强的实际应用价值。不足的是, 该算法同样依赖于用户–对象间的评分, 因此受到冷启动的限制。在未来的研究中, 应该把这种游走方式应用到更多的领域, 比如解决冷启动和数据稀疏性等问题。

参考文献
[1] Pazzani M J, Billsus D. Content-Based Recommendation Systems [A]//Brusilovsky P, Kobsa A, Nejdl W. The Adaptive Web [M]. Berlin: Springer, 2007: 325-341. [本文引用:1]
[2] Degemmis M, Lops P, Semeraro G. A Content-Collaborative Recommender that Exploits Wordnet-based User Profiles for Neighborhood Formation[J]. User Modeling and User-Adapted Interaction, 2007, 17(3): 217-255. [本文引用:1] [JCR: 1.6]
[3] Chen Y, Cheng L. A Novel Collaborative Filtering Approach for Recommending Ranked Items[J]. Expert Systems with Applications, 2008, 34(4): 2396-2405. [本文引用:1] [JCR: 1.854]
[4] Konstan J A, Miller B N, Maltz D, et al. GroupLens: Appl-ying Collaborative Filtering to Usenet News[J]. Communica-tions of the ACM, 1997, 40(3): 77-87. [本文引用:1]
[5] Herlocker J L, Konstan J A, Terveen L G, et al. Evaluating Collaborative Filtering Recommender Systems[J]. ACM Transactions on Information System (TOIS), 2004, 22(1): 5-53. [本文引用:2]
[6] Guo G. Improving the Performance of Recommender Systems by Alleviating the Data Sparsity and Cold Start Problems[C]. In: Proceedings of the 23rd International Joint Conference on Artificial Intelligence. 2013: 3217-3218. [本文引用:1]
[7] Guo G. Resolving Data Sparsity and Cold Start in Recom-mender Systems [C]. In: Proceedings of the 20th International Conference on User Modeling, Adaptation and Personaliza-tion. 2012: 361-364. [本文引用:1]
[8] Zhou T, Ren J, Medo M, et al. Bipartite Network Projection and Personal Recommendation[J]. Physical Review E, 2007, 76: Article No. 046155. [本文引用:5] [JCR: 2.313]
[9] Zhang Y C, Blaitner M, Yu Y. Heat Conduction Process on Community Networks as a Recommendation Model[J]. Physical Review Letters, 2007, 99(15): Article No. 154301. [本文引用:1] [JCR: 7.943]
[10] Guo G, Zhang J, Thalmann D, et al. From Ratings to Trust: An Empirical Study of Implicit Trust in Recommender Systems [C]. In: Proceedings of the 29th Annual ACM Symposium on Applied Computing, 2014: 248-253. [本文引用:1]
[11] Guo G, Erdt M H, Lee B S. A Hybrid Recommender System Based on Material Concepts with Difficulty Levels [C]. In: Proceedings of the 21st International Conference on Computers in Education. 2013. [本文引用:1]
[12] Morales J M, Peis E, Herrera-Viedma E. A Filtering and Recommender System for E-Scholars[J]. International Journal of Technology of Enhanced Learning, 2010, 2(2): 227-240. [本文引用:1]
[13] Guo G. Integrating Trust and Similarity to Ameliorate the Data Sparsity and Cold Start for Recommender Systems [C]. In: Proceedings of the 7th ACM Conference on Recommender Systems. ACM, 2013: 451-454. [本文引用:1]
[14] 刘淇, 陈恩红. 结合二部图投影与排序的协同过滤[J]. 小型微型计算机系统, 2010, 31(5): 835-839.
Liu Qi, Chen Enhong. Collaborative Filtering Through Combining Bipartite Graph Projection Ranking[J]. Journal of Chinese Computer Systems, 2010, 31(5): 835-839. [本文引用:4] [CJCR: 0.46]
[15] Fouss F, Pirotte A, Renders J M, et al. Rand om-Walk Computation of Similarities Between Nodes of a Graph with Application to Collaborative Recommendation[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(3): 355-369. [本文引用:1] [JCR: 1.892]
[16] Moffat A, Zobel J. Rank-based Precision for Measurement of Retrieval Effectiveness[J]. Transactions on Information Systems (TOIS), 2008, 27(1): Article No. 2. [本文引用:3]