考虑航线特征的机票价格预测方法研究*

doi:10.11925/infotech.2096-3467.2019.0522

考虑航线特征的机票价格预测方法研究^*

钟丽珍¹, 马敏书^,^,¹, 周长锋²

¹北京交通大学交通运输学院北京 100044

²中国国家铁路集团有限公司客运部北京 100033

Forecasting Airfare Based on Route Characteristics

Zhong Lizhen¹, Ma Minshu^,^,¹, Zhou Changfeng²

¹School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China

²Passenger Transport Department, China State Railway Group Co., Ltd., Beijing 100033, China

通讯作者: 马敏书,ORCID：0000-0001-8402-1199,E-mail:mshma@bjtu.edu.cn。

收稿日期: 2019-05-16 修回日期: 2019-08-1 网络出版日期: 2020-02-25

基金资助:

*本文系国家重点研发计划项目“铁路客货运效益与服务水平提高技术”. 2018YFB1201402
中国铁路总公司科技研究开发计划项目“面向铁路客运经营与服务的大数据关键技术研究”的研究成果之一. 2017X004-C

Received: 2019-05-16 Revised: 2019-08-1 Online: 2020-02-25

摘要

【目的】 对日均航班数较少且历史数据不完整甚至缺失的航线进行票价预测,辅助旅客进行购票时间决策。【方法】 借助多条航线的历史数据解决这类航线的票价预测问题。基于前人研究以及数据的可获得性,提取一批可能与机票价格波动相关的特征变量;对这些变量进行分类并利用控制变量的思想,逐步找出最合适的机票价格预测模型。【结果】 模型中包含与年度相关的变量（航程变量、航线的社会经济特征）时,其预测误差小于不包含的情况。【局限】 没有考虑中转航班等因素;没有研究居民可支配收入等特征变量;没有引入更多的预测算法和模型评价指标。【结论】 年度相关特征、两地间航程以及航线的社会经济特征均与机票价格波动相关。

关键词： 机票价格预测 ; 支持向量回归 ; 购票时间决策 ; 航线特征

Abstract

[Objective] This paper predicts airfare on routes with fewer daily average flights and incomplete or even no historical data, aiming to help passengers choose better ticketing time.[Methods] We used historical data of multiple routes to predict airfares of the targets. Based on previous research and data, we extracted characteristic variables related to airfare fluctuations. We also classified these variables to establish the airfare forecasting model.[Results] When the model contains variables like the distance and the socio-economic characteristics of the route, the prediction error was significantly reduced.[Limitations] We did not include transit flights and local residents’ income data in our study. More research is needed to evaluate the performance of predicting algorithms.[Conclusions] The characteristics related to the year, the distance between the two places and the socio-economic factors of the routes are the main reasons for airfare fluctuations.

Keywords： Airfare Prediction ; Support Vector Regression ; Ticket Purchase Time Decision ; Route Characteristic

PDF (783KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

钟丽珍, 马敏书, 周长锋. 考虑航线特征的机票价格预测方法研究^*. 数据分析与知识发现[J], 2020, 4(2/3): 192-199 doi:10.11925/infotech.2096-3467.2019.0522

Zhong Lizhen, Ma Minshu, Zhou Changfeng. Forecasting Airfare Based on Route Characteristics. Data Analysis and Knowledge Discovery[J], 2020, 4(2/3): 192-199 doi:10.11925/infotech.2096-3467.2019.0522

1 引言

随着民航的快速发展,飞机逐渐成为人们出行的重要交通工具之一。与铁路客票实施统一定价不同,航空公司为实现收益最大化,往往会在原有的定价策略下根据供需情况对机票价格实行动态浮动。即预售期内,机票价格处于不断变化中。因为旅客乘坐飞机出行的需求在时空分布上是有规律的,所以机票价格的变化也会有一定规律。因而对价格敏感型旅客来说,如何根据出行计划,选择合适的购票时间,获得低折扣的机票成为出行前需考虑的问题之一。

对于上述问题,国内外不少学者都有所研究,其研究思路主要分为两种：

（1）视为分类问题,直接给出当前时间下“购买”或“等待”的建议。Etzioni等^[1]用堆叠泛化的方法将规则学习、强化学习以及时间序列分析这几个弱分类器组合起来,构造出Hamlet算法,用该算法预测特定航线之间的航班未来几天的机票价格走势,并给出“购买”或“等待”的建议。Wohlfarth等^[2]则先用标记点过程（Marked Point Processes,MPP）的预处理技术,筛选出机票价格序列中显著变化的点,减少数据集大小,基于简化的数据求出未来一段时间价格下降的概率,并给出“购买”或“等待”的建议。

（2）视为回归问题,预测出未来一段时间的机票价格,让旅客自行选择合适的购票时间。在机器学习兴起之前,不少学者采用时间序列分析方法预测机票价格的变化趋势^[3]。随着机器学习的兴起,一些学者开始将机器学习的方法应用于此领域。Tziridis等^[4]用多层神经网络等8种机器学习方法预测机票价格,然后通过遗一法（One-Leave-Out Rule）探索不同方法在机票价格预测中的鲁棒性以及出发时间等8个特征变量在机票价格预测中的重要性;Chen等^[5]、Xu等^[6]则在历史数据的基础上引入实时机票价格数据并考虑到机票价格序列随着时间的变化而产生的参数权重变更问题。但二者的解决思路不同,前者是利用Learn++.TS算法预测机票价格,后者则是通过引入决策阈值θ,将Percentage（预测中低价天数与预测的天数之比,其中低价是指比当前票价便宜）与θ作比较,实时给出购票建议。

上述方法均是利用某一航线的历史数据实现对该航线未来价格的预测。但对于日均航班数较少的航线,对应的历史数据可能过少甚至缺失,从而导致这些方法不能适用。本文所要研究的正是如何针对这类航线进行机票价格预测的问题,为此,利用多条航线的历史数据,通过与票价波动相关特征变量的有机组合,构造出合适的预测模型。

2 建立模型

2.1 选取特征变量

预测机票价格,首先需要获得与机票价格波动相关的因素。文献[1]研究航班号、距离起飞小时数以及航空公司等因素;文献[4]研究起飞时间、到达时间以及经停次数等因素。但是以往研究大多是针对特定航线,即：其选取的变量,基本上只有航班特征,而不包括航线特征。本文要解决的问题是：如何在特定航线的历史数据较少或缺失的条件下,利用多条航线的历史数据预测其机票价格。也就是说,本研究会涉及到不同航线,而航线的特征可能与机票价格的波动有关,因而需要提取一些能够表征航线的变量。在研究机票价格的文献中基本上没有提及航线特征,但在其他文献中,有些涉及到城市特征的描述,如：文献[7]从人口数、就业率以及基础设施的布局等方面描述;文献[8]则从城市化水平、人均GDP以及第三产业占比情况等方面描述。

基于数据的可获得性,选取城市等级、人均GDP、人口数、航程、高铁单位里程票价及高铁日均开行班次这6个变量表征航线。其中,城市等级反映了城市在政治、经济以及文化等方面的综合情况;人均GDP与居民的支付能力相关;人口数则可以在一定程度上反映旅客出行规模;航程与飞行成本相关;高铁单位里程票价及日均开行班次反映了高铁作为民航主要竞争交通方式,其票价水平和供给能力,这些变量都可能与机票价格的波动相关。

除上述航线特征外,选取出发钟点等8个变量表征航班,并用距离起飞天数变量表征预测周期。对于同一航线同一天出发的航班,发到时段不同,机票价格可能会不同;同时,机票价格可能呈现淡旺季之分,因而用出发日期处于年度第几周这一变量表征票价的季节特征;不同年度票价的整体水平也许会不一样,为此选用训练数据中航班出发日期与预测航班出发日期的年度之差反映训练数据对于预测数据的参考价值;周末出发或工作日出发,机票价格可能会不一样,而周一和周五恰好处于周末前后一天,其票价也可能与周二到周四不同,为此选用是否周末等变量表征票价的星期特征;对同一趟航班而言,距离起飞天数不同（航班起飞时间与购票时间之差）,其票价也可能会有区别。

基于上述分析,共提取18个特征变量作为模型构建的备选集,其汇总结果如表1所示。

表1 特征变量备选集

Table 1 Feature Alternative Set

分类			特征变量	说明
航班	发到时段		DEPART_CLOCK	出发钟点
	发到时段		ARRIVE_CLOCK	到达钟点
	出发日期	与年度相关	WEEK_OF_THE_YEAR	该年第几周
		与年度相关	YEARS_DIFF	年份之差
		与周相关	DAY_OF_THE_WEEK	星期几
			IS_MONDAY	是否周一
			IS_FRIDAY	是否周五
			IS_WEEKEND	是否周末
航线	社会经济特征		DEP_CITY_LEVEL	出发城市的城市等级
			ARR_CITY_LEVEL	到达城市的城市等级
			DEP_GDP	出发城市的人均GDP
			ARR_GDP	到达城市的人均GDP
			DEP_POPULATION	出发城市的人口数
			ARR_POPULATION	到达城市的人口数
	空间距离		DISTANCE	航程
	高铁服务水平		HSR_STD_PRICE	高铁单位里程票价
	高铁服务水平		HSR_NUM	高铁日均开行班次
预测周期			DAYS_DIFF	距离起飞天数

新窗口打开| 下载CSV

2.2 机票价格预测模型

给定数据集 $T = {(Ζ_{i}, y_{i}) | i = 1,2, \dots, N, N \in Z^{+}}$ , $Ζ_{i}$ 指特征变量备选集, $Ζ_{i} = (ζ_{i 1}, ζ_{i 2}, \dots, ζ_{i 18})$ ,而 $y_{i}$ 指对应的最低单位里程机票价格,其计算方法如公式（1）所示。

(1)

y_{i} = \min_{t^{*}} (y_{a}^{(d, t, q)} / 飞行距离)

其中, $y_{a}^{(d, t, q)}$ 表示航线为 $a$ ,出发日期为 $d$ ,起飞时刻为 $t$ ,距离起飞天数为 $q$ 的某一航班的实际票价, $t^{*}$ 指与 $t$ 最接近的整点数（例如,当 $t$ 在6:31到7:30之间, $t^{*}$ 取7）。

取 $Ζ_{i}$ 中的 $k (k \leq 18)$ 个分量构成 $Χ_{i} = (ζ_{i q_{1}}, ζ_{i q_{2}}, \dots, ζ_{i q_{k}})$ ,其中, $q_{1}, q_{2}, \dots, q_{k} \in {1,2, 3, \dots, 18}$ 且 $\forall m \neq n, q_{m} \neq q_{n}$ 。本文目标是基于给定的 ${(Χ_{i}, y_{i}) | i = 1,2, \dots, N, N \in Z^{+}}$ ,找到一个决策函数 $\hat{y} = f (Χ)$ ,使得 $\hat{y}$ 与 $y$ 的差距最小。符合要求的算法有很多,如多层神经网络（Multi-Layer Perceptron, MLP）、随机森林回归以及回归树等。本文选用e-SVR算法,其主要优点是：将回归问题转化为凸二次规划问题,从而获得全局最优解;引入核函数的概念,巧妙地解决了维数灾难问题,提高运行效率。e-SVR的实现步骤如下^[9]：

①构造决策函数,如公式（2）所示。

(2)

\hat{y} = f (Χ) = w^{T} \cdot φ (Χ) + b

其中, $w$ 是权向量, $φ (Χ)$ 是原始空间到特征空间的映射, $b$ 是偏置。

②引入拉格朗日乘子 $α, α^{*}$ ,并选取合适的惩罚参数 $C > 0$ ,不敏感损失 $ε > 0$ 以及核函数 $K (Χ_{r}, Χ_{s})$ , $r \neq s$ ,将上述问题转化为最优化问题进行求解,如公式（3）-公式（5）所示。

(3)

\min_{α, α^{*}} \frac{1}{2} \overset{N}{\sum_{r = 1}} \overset{N}{\sum_{s = 1}} (α_{r}^{*} - α_{r}) (α_{s}^{*} - α_{s}) K (Χ_{r}, Χ_{s}) +

ε \overset{N}{\sum_{r = 1}} (α_{r}^{*} + α_{r}) - \overset{N}{\sum_{r = 1}} y_{r} (α_{r}^{*} - α_{r})

(4)

s.t. \overset{N}{\sum_{r = 1}} (α_{r} - α_{r}^{*}) = 0

(5)

0 \leq α_{r}, {α^{*}}_{r} \leq C, r = 1,2, \dots, N

最优解为 $\bar{α} = {(\bar{α_{1}}, \bar{α_{1}^{*}}, \dots, \bar{α_{N}}, \bar{α_{N}^{*}})}^{T}$ 。

③选择位于开区间 $(0, C)$ 的解分量 $\bar{α}$ 或 $\bar{α^{*}}$ ,计算 $\bar{b}$ ,如公式（6）所示。

(6)

\bar{b} = y_{s} - \overset{N}{\sum_{r = 1}} (\bar{α_{r}^{*}} - \bar{α_{r}}) K (Χ_{r}, Χ_{s}) \pm ε

其中, $ε$ 前的符号由所选择的解分量决定,如果所选择的是 $\bar{α}$ ,则取“+”,反之,取“-”。

④获得决策函数,如公式（7）所示。

(7)

y = f (Χ) = \overset{N}{\sum_{r = 1}} (\bar{α_{r}^{*}} - \bar{α_{r}}) K (Χ_{r}, Χ_{s}) + \bar{b}

步骤②中涉及的核函数 $K (Χ_{r}, Χ_{s})$ 有很多种形式,本文选取较为常用的RBF核函数,其表达式如公式（8）所示。

(8)

K (Χ_{r}, Χ_{s}) = \exp (- γ {‖Χ_{r} - Χ_{s}‖}^{2}) (γ > 0)

3 实证分析

3.1 构建模型

2.1节共选取了18种特征变量,但没有必要将所有特征变量都放入模型中,原因如下：这些特征中可能包含冗余信息;特征数过多可能导致维数灾难、过拟合等问题。利用控制变量的思想,逐步找出最佳的特征组合。模型构建步骤如表2所示。

表2 模型构建过程

Table 2 The Process of Model Building

步骤	特征变量		备注
步骤	自变量	控制变量	备注
1	出发日期	空间距离高铁服务水平社会经济特征发到时段预测周期	将表征出发日期的两类变量进行组合,构造16个模型M1-M16,如表3所示。
2	空间距离	出发日期高铁服务水平社会经济特征发到时段预测周期	去掉空间距离这一变量,构造模型M17。
3	高铁服务水平	出发日期空间距离社会经济特征发到时段预测周期	将表征高铁服务水平的两个变量进行组合,构造3个模型M18-M20,如表4所示。
4	社会经济特征	出发日期空间距离高铁服务水平发到时段预测周期	将表征社会经济特征的三组变量进行组合,构造7个模型M21-M27,如表5所示。

(注：①控制变量指可能对实验结果产生影响,但在该阶段中不进行研究的变量;自变量指可能对实验结果产生影响,且在该阶段中需要研究的变量;② 表示该变量是上一步优化后的特征变量。)

新窗口打开| 下载CSV

第一步,选定出发日期作为自变量,其余的作为控制变量;然后按照表3将表征出发日期的6个变量构造出16种组合,并将其与表征空间距离等的10个变量放入特征变量集中,构造出16个模型M1-M16;利用e-SVR算法求解模型,根据误差最小原则选取最合适的特征变量组合来表征出发日期;第二步,选定空间距离作为自变量,上一步选取的出发日期特征变量组合及剩下的高铁服务水平等作为控制变量;然后将除空间距离外的所有变量放入特征变量集中,构造出模型M17;利用e-SVR算法求解模型,根据误差最小原则决定最终的模型中是否需要加入空间距离这一变量;第三、四步依此类推。

表3 出发日期的特征表示

Table 3 The Description of Depart Date

特征模型	M1	M2	M3	M4	M5	M6	M7	M8	M9	M10	M11	M12	M13	M14	M15	M16
WEEK_OF_THE_YEAR	-	√	-	√	-	√	-	√	-	√	-	√	-	√	-	√
YEARS_DIFF	-	-	√	√	-	-	√	√	-	-	√	√	-	-	√	√
DAY_OF_THE_WEEK	-	-	-	-	√	√	√	√	-	-	-	√	-	-	-	-
IS_MONDAY	-	-	-	-	-	-	-	-	-	-	-	-	√	√	√	√
IS_FRIDAY	-	-	-	-	-	-	-	-	-	-	-	-	√	√	√	√
IS_WEEKEND	-	-	-	-	-	-	-	-	√	√	√	√	√	√	√	√

(注：“√”表示对应模型中加入该特征变量,“-”与之相反,下同。）

新窗口打开| 下载CSV

经过上述4个步骤得到最优的机票价格预测模型：优化后的出发日期、空间距离、高铁服务水平、社会经济特征以及原始发到时段、预测周期。

表4 高铁服务水平的特征表示

Table 4 The Description of High-speed Rail Service Level

特征模型	M18	M19	M20
HSR_STD_PRICE	-	√	-
HSR_NUM	-	-	√

新窗口打开| 下载CSV

表5 社会经济特征的特征表示

Table 5 The Description of Socioeconomic Feature

特征模型	M21	M22	M23	M24	M25	M26	M27
DEP_CITY_LEVEL	-	√	√	-	√	-	-
ARR_CITY_LEVEL	-	√	√	-	√	-	-
DEP_GDP	-	√	-	√	-	√	-
ARR_GDP	-	√	-	√	-	√	-
DEP_POPULATION	-	-	√	√	-	-	√
ARR_POPULATION	-	-	√	√	-	-	√

新窗口打开| 下载CSV

3.2 数据与处理

采集2015年1月1日-2017年12月31日部分航线的航班信息,并从中选取广州-南宁、重庆-福州、杭州-长沙、郑州-深圳、南昌-北京、南宁-武汉以及南宁-郑州这7条航线进行研究。其中2017年12月1日-2017年12月15日的航班数据作为测试集,同时,考虑到相邻年份的机票价格可能具有相近的年度波动规律,选取上述航线2015年、2016年同期以及2017年11月的航班数据作为训练集。上述航线有以下共同点：日均航班数少且历史数据较少甚至缺失,如南宁-郑州日均航班数为7,且其训练集中13点出发的航班只有2017年的数据。

根据数据的实际情况,将出发钟点限定在8点-17点之间,距离起飞天数限定为大于15天,同时不考虑经停、共享以及廉价航班。另外,城市等级有不同的划分标准,选用由第一财经发布并被各大媒体广泛转载的版本,人均GDP及人口数则是从国家统计局网站采集。

因为原始数据中不同特征及票价取值范围相差较大,采用最大-最小值规范法对数据集中所有非二分变量进行归一化处理,映射到[0,1]区间内。方法如下：给定一个物理量 $ρ_{i}$ , $i = 1,2, \dots, N, N \in Z^{+}$ ,其中, $ρ_{i}$ 指带量纲的原始数据, ${ρ_{i}}^{*}$ 指归一化后的数据, $\max (ρ_{i})$ , $\min (ρ_{i})$ 分别表示最大值和最小值,则归一化的结果如公式（9）所示。

(9)

{ρ_{i}}^{*} = \frac{ρ_{i} - \min (ρ_{i})}{\max (ρ_{i}) - \min (ρ_{i})}

3.3 模型训练

由2.2节可知,模型求解过程主要涉及参数 $C$ 、 $ε$ 以及 $γ$ 的选取。根据既往对e-SVR的研究,各参数的取值范围如表6所示。

表6 参数取值范围

Table 6 The Value Range of Parameters

参数	取值范围
$C$	[0.001,0.01,0.1,1,10,100]
$ε$	[0.001,0.01,0.1,1,10,100]
$γ$	[ $2^{- 10}, 2^{- 9}, \dots, 2^{3}$ ]

新窗口打开| 下载CSV

评价模型结果的指标有很多,如解释方差（Explained Variance）、平均绝对值误差（Mean Absolute Deviation, MAE）等,而本文将平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）作为参数选取的标准,以5折交叉验证的方式选出最优参数。其计算方法如公式（10）所示。

(10)

e = \frac{1}{l} \overset{l}{\sum_{i = 1}} \frac{|{\hat{y}}_{i} - y_{i}|}{y_{i}} \times 100 %

其中, $e$ 是误差值; $y_{i}$ 表示实际票价; ${\hat{y}}_{i}$ 是预测票价; $l$ 代表样本个数。选取使得误差值最小且参数值最小的 $C$ 、 $ε$ 、 $γ$ 作为最终的模型参数进行预测。

3.4 结果分析

采用3.3节的误差公式作为模型的评价指标,并对部分误差分布进行显著性检验,其中威尔科克森符号秩检验适用于两配对样本的检验,而傅莱德曼检验适用于多配对样本的检验。当检验结果P值小于0.05时,可拒绝原假设,即：认为在95%的置信度下,检验样本的分布有显著差异。

（1）出发日期相关变量选取对预测误差的影响分析

在其他特征变量一定的情况下,为分析出发日期相关变量的选取对预测误差的影响,共构建16个模型,其预测误差如表7所示。

表7 出发日期不同表示方式的误差对比

Table 7 Errors with Different Descriptions of Departure Date

与年度相关与周相关	-	DAY_OF_THE_WEEK	IS_WEEKEND	IS_MONDAY IS_FRIDAY IS_WEEKEND
与年度相关与周相关	误差（模型）	误差（模型）	误差（模型）	误差（模型）
-	28.90%(M1)	19.87%(M5)	29.72%(M9)	26.51%(M13)
WEEK_OF_THE_YEAR	19.14%(M2)	19.60%(M6)	19.65%(M10)	19.70%(M14)
YEARS_DIFF	21.64%(M3)	13.59%(M7)	22.69%(M11)	14.36%(M15)
WEEK_OF_THE_YEAR YEARS_DIFF	13.39%(M4)	13.89%(M8)	14.24%(M12)	20.78%(M16)

(注：①“-”表示模型中不包含该类型的变量,下同;②加粗数字表示该列的最小值,下同;③带下划线数字表示该行的最小值,下同。）

新窗口打开| 下载CSV

从表7可以看出,当模型中包含“YEARS_ DIFF”变量时的预测误差显著小于不包含的时候,也就是说,机票价格波动与年度相关。此外,当模型中有“DAY_OF_THE_WEEK”变量时,预测误差较小,即机票价格波动与出发日期在星期中的位置有关。此外,M4、M7、M8这三个模型的预测误差都比较小,对它们进行显著性检验发现,三者并无显著性差异（P值为0.139）,因而选取误差值最小且特征数相对较少的模型M4作为后续研究的基础。

（2）航线相关变量选取对预测误差的影响分析

在M4的基础上,为分析航线相关变量选取对预测误差的影响,共构建11个模型,其预测误差如表8-表10所示。由表8可知,模型中包含航程变量时,预测误差小于不包含的时候,换句话说,机票价格波动与两地之间的航程有关。从表9可知,各模型之间的预测误差相差不大,也就是说,机票价格波动与高铁标准票价及高铁日均开行班次不相关。为简化模型,接下来的研究中不考虑这两个变量。

表8 模型中是否包含航程的误差对比

Table 8 Errors Considering Whether Distance is Included in the Models

	误差（模型）
有DISTANCE	13.39%(M4)
无DISTANCE	16.19%(M17)

新窗口打开| 下载CSV

表9 高铁服务水平不同表示方式的误差对比

Table 9 Errors with Different Descriptions of High-speed Rail Service Level

	有HSR_NUM	无HSR_NUM
	误差（模型）	误差（模型）
有HSR_STD_PRICE	13.39%(M4)	13.37%(M20)
无HSR_STD_PRICE	13.37%(M19)	13.33%(M18)

新窗口打开| 下载CSV

由表10可以看出：

表10 社会经济特征不同表示方式的误差及P值对比

Table 10 Errors and P-values with Different Descriptions of Socioeconomic Feature

社会经济特征	误差	模型	P值
社会经济特征	误差	模型	M18	M21	M22	M23	M24	M25	M26
ALL	13.33%	M18	-	-	-	-	-	-	-
NONE	24.12%	M21	0.000*	-	-	-	-	-	-
CITY_LEVEL+GDP	13.43%	M22	0.388	0.000*	-	-	-	-	-
CITY_LEVEL+PLN	13.15%	M23	0.582	0.000*	0.076	-	-	-	-
GDP+PLN	13.26%	M24	0.315	0.000*	0.204	0.709	-	-	-
CITY_LEVEL	13.51%	M25	0.395	0.000*	0.515	0.021*	0.163	-	-
GDP	20.36%	M26	0.000*	0.035*	0.000*	0.000*	0.000*	0.000*	-
PLN	17.68%	M27	0.001*	0.000*	0.001*	0.000*	0.000*	0.000*	0.045*

(注：①CITY_LEVEL包括DEP_CITY_LEVEL和ARR_CITY_LEVEL;②GDP包括DEP_GDP和ARR_GDP;③PLN包括DEP_POPULATION和ARR_POPULATION;④ALL包括CITY_LEVEL、GDP以及PLN;⑤NONE指不含任一个社会经济特征变量;⑥*表示P值小于0.05。）

新窗口打开| 下载CSV

①当模型中不包含表征航线社会经济特征的变量时,误差显著大于包含时,也就是说,机票价格波动与航线的社会经济特征有关。

②当模型中仅用一组变量表征航线社会经济特征时,用CITY_LEVEL这组变量的误差显著小于用GDP或PLN时的误差。而且,仅用CITY_LEVEL这组变量与用三组变量表征航线社会经济特征,二者的预测误差没有显著差异,都显著小于不包含任一组表征航线社会经济特征的变量时的误差。因此,如果只能选取一组变量表征航线社会经济特征,应当选用CITY_LEVEL这组变量。与GDP和PLN相比,机票价格波动与航线的城市等级相关性更强。

③当模型中仅用两组变量表征航线社会经济特征时,三者的预测误差均比较小且无显著差异。同时,三者与包含所有表征航线社会经济特征的变量的模型预测误差并无显著差异,且其预测结果显著优于不包含任一组表征航线社会经济特征的变量的模型的预测结果。因此,如果选取两组变量表征航线社会经济特征,任一组合均可。

④两两组合的预测误差均小于仅用CITY_ LEVE这组变量时的预测误差,但只有CITY_ LEVEL和PLN这个组合的误差分布与其误差分布具有显著差异,所以本文用城市等级以及人口数表征航线社会经济特征,一方面该模型（M23）预测误差最小,另一方面没有将所有表征航线社会经济特征的变量纳入模型,模型更加简洁。

（3）混合航线与单航线的预测误差对比分析

通过控制变量法选出一个相对较优的预测模型（M23）。为进一步验证该模型,将此模型的预测误差与对单条航线进行训练预测的误差进行对比分析。其预测误差如表11所示。

表11 混合航线与单航线的预测误差对比

Table 11 Prediction Errors Between Mixed Routes and Single Routes

航线	混合航线	单条航线	误差之差
南宁-郑州	18.78%	33.74%	-14.96%
重庆-福州	5.48%	13.45%	-7.97%
南宁-武汉	6.30%	9.60%	-3.30%
南昌-北京	20.76%	19.58%	1.18%
杭州-长沙	4.86%	3.63%	1.23%
郑州-深圳	7.90%	2.34%	5.56%
广州-南宁	15.79%	1.54%	14.25%

新窗口打开| 下载CSV

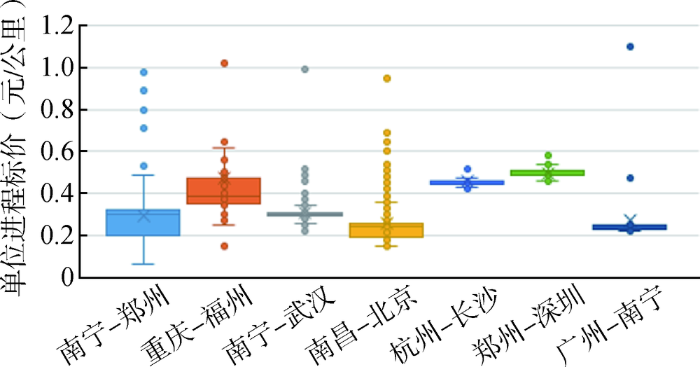
对于南宁-郑州、重庆-福州及南宁-武汉,多航线混合的预测结果要优于单航线的预测结果;对南昌-北京、杭州-长沙来说,两种预测方法的误差相差不大;而对郑州-深圳和广州-南宁而言,多航线混合训练预测的误差大于单航线训练预测的误差。

各航线单位里程票价分布如图1所示,各航线数据集如表12所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 各航线单位里程票价分布情况

Fig.1 Distribution of Airfares per Mileage

表12 各航线数据集情况

Table 12 Data Set of Every Route

航线	测试集中具有不同年份的历史同期数据的占比			测试集中具有近期数据的占比
航线	2年	1年	没有	测试集中具有近期数据的占比
南宁-郑州	8%	23%	12%	57%
重庆-福州	9%	9%	9%	73%
南宁-武汉	42%	0%	14%	44%
南昌-北京	16%	8%	7%	69%
杭州-长沙	-	-	-	100%
郑州-深圳	-	-	-	100%
广州-南宁	-	-	-	100%

(注：“-”表示该航线测试集不具备历史同期数据。）

新窗口打开| 下载CSV

由图1可以看出,与南宁-郑州、重庆-福州及南昌-北京这3条航线相比,南宁-武汉等4条航线的票价较为集中,波动较小。而从表12可知,与南宁-郑州、重庆-福州、南宁-武汉及南昌-北京这4条航线相比,杭州-长沙等3条航线训练集数据偏少且均没有历史同期数据。由此可以推测,在多航线混合预测模型中,票价波动大的航线可能会对票价波动小的航线的预测准确度造成影响,使得该航线的预测误差变大,因而,本文模型比较适用于票价波动较大的航线。

4 结语

围绕对历史数据较少或者缺失的航线进行机票价格预测的问题,本文主要完成了以下工作：

（1）基于前人研究以及数据的可获得性,选取出与机票价格波动相关的特征变量;

（2）以特征变量分类为基础,利用控制变量的思想,通过多次迭代,实现了特征变量的筛选及组合,以逐步形成最合适的机票价格预测模型;

（3）根据预测结果,分析与机票价格波动有关的变量。实证结果表明：对于这类航线的票价预测,与年度相关的变量比与周相关的变量更重要,即同一航线不同年度之间的机票价格波动规律更相似;其机票价格波动与两地之间的航程显著相关,但与高铁服务水平不相关;其票价波动也与航线的社会经济特征有关。此外,从本文选出的多航线混合的机票价格预测模型与单航线模型的对比中发现,多航线混合的模型在票价波动较大的航线上的预测效果更好,也就是说,本文所提模型更适用于历史数据不全甚至缺失、但票价波动大的航线。

由于能力、时间、数据等方面的限制,本研究存在诸多不足之处,主要表现在：没有考虑共享、中转以及廉价航班;没有对更多的特征变量进行研究,如居民可支配收入等;预测算法及模型评价方法太过单一,没有引入更多的算法和模型评价指标。未来研究将弥补这些方面的不足,希望获得更好的结果。

作者贡献声明

钟丽珍：设计算法,清洗和分析数据,撰写论文;

马敏书：提出研究思路,设计研究方案,修改论文;

周长锋：采集数据,修改论文。

利益冲突声明

所有作者声明不存在利益冲突关系。

支撑数据

支撑数据由作者自存储, E-mail: tanglin@dlut.edu.cn。

支撑数据由作者自存储,E-mail: 17120979@bjtu.edu.cn。

[1] 钟丽珍.airfare_prediction.zip. 机票价格预测分析及结果数据.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Etzioni

, Tuchinda

, Knoblock

, et al.

To Buy or Not to Buy: Mining Airfare Data to Minimize Ticket Purchase Price

[C]// Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2003: 119-128.

[本文引用: 2]

[2]

Wohlfarth

, Clémençon

, Roueff

, et al.

A Data-Mining Approach to Travel Price Forecasting

[C]// Proceedings of the 10th International Conference on Machine Learning & Applications & Workshops. 2011: 84-89.

[本文引用: 1]

[3]

顾兆军, 王双, 赵亿 .

基于时间序列的机票价格预测模型

[J]. 中国民航大学学报, 2013,31(2):80-84.

[本文引用: 1]

( Gu

Zhaojun

, Wang

Shuang

, Zhao

Flight Ticket Fare Prediction Model Based on Time-Serial

[J]. Journal of Civil Aviation University of China, 2013,31(2):80-84.)

[本文引用: 1]

[4]

Tziridis

, Kalampokas

, Papakostas G

, et al.

Airfare Prices Prediction Using Machine Learning Techniques

[C]// Proceedings of the 25th European Signal Processing Conference. 2017: 1036-1039.

[本文引用: 2]

[5]

Chen

, Cao

, Feng

, et al.

An Ensemble Learning Based Approach for Building Airfare Forecast Service

[C]// Proceedings of the 2015 IEEE International Conference on Big Data. 2015: 964-969.

[本文引用: 1]

[6]

, Cao

OTPS: A Decision Support Service for Optimal Airfare Ticket Purchase

[C]// Proceedings of the 2017 IEEE International Conference on Big Data. 2017: 1363-1368.

[本文引用: 1]

[7]

王振, 张志敏, 禚保玲 .

基于多源数据的青岛市中心城区城市特征研究

[C]//2018中国城市规划年会. 2018.

[本文引用: 1]

( Wang

Zhen

, Zhang

Zhimin

, Zhuo

Baoling

Research on the Urban Characteristics of Qingdao City Center Based on Multi-source Data

[C]//Proceedings of 2018 China Urban Planning Annual Meeting. 2018.

[本文引用: 1]

[8]

卢晓涵, 罗吉, 琚瑞 , 等.

基于区域竞争力的国家中心城市特征研究

[C]//2018中国城市规划年会. 2018.

[本文引用: 1]

( Lu

Xiaohan

, Luo

, Ju

Rui

, et al.

Research on the Characteristics of National Central Cities Based on Regional Competitiveness

[C]//Proceedings of 2018 China Urban Planning Annual Meeting. 2018.

[本文引用: 1]

[9]

, Lin Y

, Chen

, et al.

Microstructural Evolution and Support Vector Regression Model for an Aged Ni-Based Superalloy During Two-Stage Hot Forming with Stepped Strain Rates

[J]. Materials & Design, 2018,154:51-62.

[本文引用: 1]

To Buy or Not to Buy: Mining Airfare Data to Minimize Ticket Purchase Price

2003

... （1）视为分类问题,直接给出当前时间下“购买”或“等待”的建议.Etzioni等^[1]用堆叠泛化的方法将规则学习、强化学习以及时间序列分析这几个弱分类器组合起来,构造出Hamlet算法,用该算法预测特定航线之间的航班未来几天的机票价格走势,并给出“购买”或“等待”的建议.Wohlfarth等^[2]则先用标记点过程（Marked Point Processes,MPP）的预处理技术,筛选出机票价格序列中显著变化的点,减少数据集大小,基于简化的数据求出未来一段时间价格下降的概率,并给出“购买”或“等待”的建议. ...

... 预测机票价格,首先需要获得与机票价格波动相关的因素.文献[1]研究航班号、距离起飞小时数以及航空公司等因素;文献[4]研究起飞时间、到达时间以及经停次数等因素.但是以往研究大多是针对特定航线,即：其选取的变量,基本上只有航班特征,而不包括航线特征.本文要解决的问题是：如何在特定航线的历史数据较少或缺失的条件下,利用多条航线的历史数据预测其机票价格.也就是说,本研究会涉及到不同航线,而航线的特征可能与机票价格的波动有关,因而需要提取一些能够表征航线的变量.在研究机票价格的文献中基本上没有提及航线特征,但在其他文献中,有些涉及到城市特征的描述,如：文献[7]从人口数、就业率以及基础设施的布局等方面描述;文献[8]则从城市化水平、人均GDP以及第三产业占比情况等方面描述. ...

A Data-Mining Approach to Travel Price Forecasting

2011

基于时间序列的机票价格预测模型

2013

... （2）视为回归问题,预测出未来一段时间的机票价格,让旅客自行选择合适的购票时间.在机器学习兴起之前,不少学者采用时间序列分析方法预测机票价格的变化趋势^[3].随着机器学习的兴起,一些学者开始将机器学习的方法应用于此领域.Tziridis等^[4]用多层神经网络等8种机器学习方法预测机票价格,然后通过遗一法（One-Leave-Out Rule）探索不同方法在机票价格预测中的鲁棒性以及出发时间等8个特征变量在机票价格预测中的重要性;Chen等^[5]、Xu等^[6]则在历史数据的基础上引入实时机票价格数据并考虑到机票价格序列随着时间的变化而产生的参数权重变更问题.但二者的解决思路不同,前者是利用Learn++.TS算法预测机票价格,后者则是通过引入决策阈值θ,将Percentage（预测中低价天数与预测的天数之比,其中低价是指比当前票价便宜）与θ作比较,实时给出购票建议. ...

基于时间序列的机票价格预测模型

2013

Airfare Prices Prediction Using Machine Learning Techniques

2017

An Ensemble Learning Based Approach for Building Airfare Forecast Service

2015

OTPS: A Decision Support Service for Optimal Airfare Ticket Purchase

2017

基于多源数据的青岛市中心城区城市特征研究

2018

基于多源数据的青岛市中心城区城市特征研究

2018

基于区域竞争力的国家中心城市特征研究

2018

基于区域竞争力的国家中心城市特征研究

2018

Microstructural Evolution and Support Vector Regression Model for an Aged Ni-Based Superalloy During Two-Stage Hot Forming with Stepped Strain Rates

2018

... 取

Ζ_{i}

中的

k (k \leq 18)

个分量构成

Χ_{i} = (ζ_{i q_{1}}, ζ_{i q_{2}}, \dots, ζ_{i q_{k}})

,其中,

q_{1}, q_{2}, \dots, q_{k} \in {1,2, 3, \dots, 18}

且

\forall m \neq n, q_{m} \neq q_{n}

.本文目标是基于给定的

{(Χ_{i}, y_{i}) | i = 1,2, \dots, N, N \in Z^{+}}

,找到一个决策函数

\hat{y} = f (Χ)

,使得

\hat{y}

与

y

的差距最小.符合要求的算法有很多,如多层神经网络（Multi-Layer Perceptron, MLP）、随机森林回归以及回归树等.本文选用e-SVR算法,其主要优点是：将回归问题转化为凸二次规划问题,从而获得全局最优解;引入核函数的概念,巧妙地解决了维数灾难问题,提高运行效率.e-SVR的实现步骤如下^[9]： ...

〈

〉