近年, 公共危机和风险防控越来越受到政府和大众的关注, 而监狱作为国家刑罚执行机关, 关押着触犯法律的罪犯, 包括被判处无期徒刑、死缓的重案犯, 是公共治安危险程度最集中的地方, 是最需要加强管理调控风险的行政机关。为吸取各类监狱安全事故的沉痛教训, 中国多个省监狱系统明确要求必须抓紧建立监狱安全风险危机管理机制^[1]。对监狱安全的管理分为事前、事中和事后, 其中最为重要的环节是事前预防。预防性风险管理能有效减少监狱安全威胁事件的发生, 而监狱风险评估是预防性风险管理的重要环节, 其主要内容是对监狱内部风险因素进行评估, 进而预防风险。其中, 监犯风险评估, 即对监犯在狱中的行为风险进行分析评估, 是监狱内部风险评估的主要内容。

目前监犯风险评估主要方法有问卷调查法^[2,3,4]、回归预测^[5,6]和定性定量相结合等方法^[7,8,9]。现有问卷分为监犯自评和管理人员他评, 虽然是最方便的评价方法, 但马国富等^[4]通过对国内外服刑人员的危险性及其再犯罪评估现状的梳理, 发现基于量表的传统服刑人员危险性评估工具的适应性和精确性受到挑战, 存在虚假作答和主观性过强的问题, 科学性有所欠缺; 曾赟^[6]对浙江省不同类型监狱1 238名随机在押犯样本进行调查与统计, 采用多因素方差分析与二元Logistic回归分析, 提出11项罪犯出监前重新犯罪预测因子, 但没有给出预测因子与应变量(再犯罪)的函数关系, 故回归预测可以初步发现与风险有关的因素, 但其变量之间的函数关系难以确定, 且最后得到的准确率较低, 因此有效性尚待提高; 定性与定量相结合的评价方法一定程度上解决了以上两种方法的问题, 既能避免主观性过强, 又能提高评估准确性, 相较而言是更为科学有效的评估方法, 但此方法依然存在可改进之处^[8,9]:

(1) 定性定量方法的结果较为模糊, 缺乏可识别性。即其结果体现了某位监犯在服刑期闹事的可能性, 但不能体现其可能犯事的行为类型, 如发生暴力行为或自杀行为等, 这使得管理人员即使知道监犯存在风险也无法进行针对性预防管理。

(2) 现有研究未考虑监狱背景下评价者的主观判断模糊性。监犯风险指标的标注多为0-1型, 而监狱背景下评价者对监犯的主观判断存在很大的模糊性, 0-1型标注不但无法体现模糊性, 还无法体现不同监犯在相关特征上的个体差异, 从而导致标注失真。标注是评价过程的数据基础, 失真会导致评价结果准确性降低。

(3) 指标定权方法已不适应现有监犯风险评估需求。定性定量方法需要制定指标以及指标定权, 但传统方法制定的指标及权值难以适应不同监狱。不同监狱背景下监犯风险的影响因素不同, 其权值自然也不尽相同。

针对问题(1), 本文提出监犯特征风险这一概念, 包括暴力型、心理问题型、教唆型和缺乏辨识型4种风险类型, 将监犯的4类风险特征的程度作为评估目标。针对问题(2), 将一种多属性决策方法区间模糊VIKOR (ViseKriterijumska I Kompromisno Optimizacija Resenje)^[10,11]应用到监犯风险评估中并进行改进, 用于处理模糊性评价集, 将区间模糊评价转化为最符合实际的评价值。针对问题(3), 结合多种机器学习算法, 对构造的监犯风险标注集进行预测建模, 构建监犯评估模型, 其预测结果可以代表监犯各风险特征的程度; 最后与现有监犯风险评估模型进行对比, 验证评估方法有效性。此监犯风险评估方法适用于不同监狱, 可通过此方法构建出符合各监狱实情的评估模型。本文以新疆某监狱提供的监犯数据为样本进行实证分析。

本文方法思路如图1所示。

流程图中第二部分引入监犯特征风险概念, 此方法主要解决风险评估结果缺乏可识别性的问题。将传统方法中对单一风险的预测转换为对4项具体的风险类型的预测。对划分后的特征分别进行标注, 再进行预测建模, 其评估结果能够体现某监犯的 不同风险类型的程度, 便于管理人员进行针对性 管理。

第二部分引入改进的区间模糊VIKOR算法, 以优化标注集准确性。4类风险特征无法通过历史数据量化, 需要综合专家判断以提高准确性与真实性, 而多属性决策(Multi-Attribute Decision-Making, MADM)方法可以结合不充分的历史数据与专家判断, 通过对标注集排序计算风险值^[12]。在排序方法方面, 常用的方法有TOPSIS、AHP、VIKOR等。TOPSIS方法没有考虑计算过程中评价对象与正负理想解距离的权重, 求得的最优解未必是最接近理想点的解^[13]; AHP难以保证方法所要求的评判信息一致; VIKOR同时考虑群体效用最大化和个体遗憾最小化, 并融入决策者主观偏好, 有助于保证决策结果的合理性^[14]。且监狱背景下专家标注的出发点不是找到特征最明显的“理想解”, 而是找到最能考虑所有专家判断结果的“折衷解”, 因此本文选择能够使得个体遗憾最小化的VIKOR算法。但传统VIKOR存在两个漏洞, 一方面, 主观判断指标的权重会造成结果的不确定性^[14]; 另一方面, 算法中“个体遗憾值”R的数值计算与指标间的相关性有关, 原算法不考虑指标间的相关性, 使得R计算值偏大, 变相扩大了“个体遗憾”的权重, 从而使得最终评价结果增加, 影响算法客观性^[15]。鉴于以上两点, 本文将VIKOR中的指标替换为相互独立的监犯风险特征, 并简化其权值计算过程。监犯风险特征无重要性区分, 避免了指标赋权造成的结果误差; 特征间相互独立, 减少了指标间相关而造成的R值偏差。

第三部分用机器学习算法旨在解决指标定权难以统一的问题。机器学习算法能够根据数据训练建模, 从而产生适合此数据集的相关参数, 避免统一定权的问题。不同监狱可根据自身关押的监犯的数据产生适合本监狱的模型, 还能根据参数判断本监狱影响监犯风险的关键因素。

本研究的监犯风险评估流程如下:

(1) 进行数据预处理, 筛选出可能影响监犯风险的数据项, 并划分为待标注数据集(训练集与测试集)和评估效果验证集。其中, 待标注数据集是从原数据集中随机选取的213位监犯数据集, 用于训练模型; 评估效果验证集指从剩余数据集中选取的带有“处遇等级”标签的660位监犯数据集, 用于验证模型有效性。“处遇等级”作为判断监犯是否犯事的依据, 用于模型评估效果验证。

(2) 组织4位监狱专家对待标注数据集中监犯的特征风险分别进行0-1区间模糊性标注, 然后利用区间模糊VIKOR计算标注集, 以监犯的4类特征风险为决策属性, 以不同评价者对监犯的评价作为决策对象, 其排序第一的评价方案是每位监犯最符合实际的特征标注, 之后将结果转化为可训练数据集。

(3) 考虑各机器学习算法对不同风险特征的适应性不同, 且各监犯个人的特征类型相互独立, 故运用多种机器学习算法对处理后的训练集各风险特征分别进行训练建模, 以拟合优度最高的模型为各特征最终评估模型, 通过此模型可根据监犯数据评估所有监犯的4项特征风险。

(4) 将训练好的综合监犯特征风险评估模型用于评估效果验证集, 评估模型的泛化性。同时将已有研究成果应用于同一验证集, 与本文模型对比。

大量事实表明, 监狱风险事件具有明显特征^[6,7], 大致可以分为暴力事件、自杀行为、有组织的群体危险性行为(如集体礼拜)等。这些事件往往都是由相似特征的监犯所制造。对监犯特征进行分类可以根据其特性预防相应风险事件, 这种反映风险事件制造者特征的分类策略, 本文称之为监犯特征风险。

以往对监犯的危险性评估都建立在单一危险性上, 即评估此监犯做出危害事件的风险性, 但无法识别其所犯风险事件类型。经文献研究以及与业内专家交流, 本文将监犯的危险性分为4类倾向, 分别是暴力型、心理问题型、教唆他人型、缺乏辨识型。不同监犯的4类特征之间具有相关性。将单一监犯风险划分为4类监犯特征风险具有重大意义:

(1) 多类特征是引入多属性决策(MADM)方法解决风险评估问题的模型基础。区间模糊VIKOR算法以4类特征风险倾向作为犯人决策属性, 以不同专家对每个犯人4类倾向的区间模糊打分作为决策方案。传统单一风险无法构成多属性, 无法引入MADM。

(2) 特征间相互独立是改进区间模糊VIKOR算法的理论基础。监犯个体的4类特征之间互不影响且无重要性区分, VIKOR算法的特征指标间独立可以避免指标赋权和R值计算带来的偏差。

(3) 监犯特征是监狱智慧管理的数据支持和科学依据。一方面, 监犯特征评估结果可以为监犯针对性管理提供数据支持; 另一方面, 为后续研究监犯间交互、改善监舍分布、降低监舍风险提供了理论基础与方法。

本文特征分类策略来源于对大量文献的总结, 因此并不只适用于新疆监狱, 也可以适应全国绝大部分监狱, 其相应特征如表1所示。

需要注意的是, 本文将犯人风险分为4种类型, 不代表每个犯人都是这4类风险类型之一。这意味着会有在狱中表现较好, 或者本身所犯罪名并不严重的犯人, 他们并不存在明显的风险表征; 也会有犯人属于多种风险类型, 如典型的“炮手”, 这类人既缺乏辨识能力, 又具有暴力倾向, 他们同时属于暴力型和缺乏辨识型。

VIKOR^[11]方法是由Opricovic提出的一种基于理想点解的折衷型多准则决策方法, 其基本原理是: 通过确定各准则下的正理想解和负理想解, 再根据各个方案的评价值与正理想解的接近程度, 在可接受优势和决策过程稳定的条件下对方案进行排序, 即根据“折衷”程度对方案进行排序。本文将具有重要性区分的指标替换为无重要性区分的监犯风险特征, 简化了算法过程中的指标计算。原公式由Sayadi等^[10]提出, 公式(1)、公式(4)和公式(5)为原公式, 公式(2)和公式(3)为改进的公式。改进的区间数型模糊VIKOR方法的步骤如下。

(1) 建立区间数型指标决策矩阵:

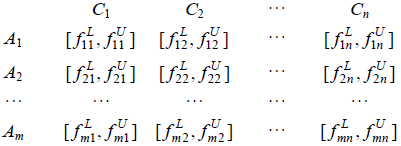
其中, A₁, A₂, ···, A_m是标注方案, C₁, C₂, ···, C_n表示评估对象的n个相互独立特征, $[f_{ij}^{L},f_{ij}^{U}]$是第i个方案的第j个特征值, 此时特征值为区间数。

(2) 确定被评价对象集的正理想解${{f}^{+}}$和负理想解${{f}^{-}}$, 计算方法如公式(1)所示^[10]。

其中, I和J分别为效益型评价准则集合和成本型评价准则集合, n为指标的总个数。

(3) 确定被评价对象的群体效益区间值${{S}_{i}}=[S_{i}^{L},S_{i}^{U}]$和个体遗憾区间值${{R}_{i}}=[R_{i}^{L},R_{i}^{U}]$, 在Sayadi等^[10]所提公式的基础上进行改进, 省略了指标权值$w$的计算。改进的计算公式如公式(2)和公式(3)所示。

(4) 确定被评价对象的利益比率区间值${{Q}_{i}}=[Q_{i}^{L},Q_{i}^{U}]$, 计算方法如公式(4)所示^[10]。

其中, v是决策机制系数(v取值为0.5, 表明采 用均衡折衷方式, 可以使群体效用最大化和负面影 响最小化); ${{S}^{-}}=\max S_{I}^{U}$, ${{S}^{+}}=\min S_{I}^{L}$, ${{R}^{-}}=\max R_{I}^{U}$, ${{R}^{+}}=\min R_{I}^{L}$^[10]。

(5) 根据${{Q}_{j}}$、${{S}_{j}}$和${{R}_{j}}$的值对被评价对象进行排序。当满足以下两个条件时, 可根据${{Q}_{j}}$的大小排序, ${{Q}_{j}}$值越小, 第j个被评价对象排序越靠前。${{Q}_{j}}$的计算方法如公式(5)所示^[10]。

①$Q({{k}^{(2)}})-Q({{k}^{(1)}})\ge 1/(m-1)$, 其中, ${{k}^{(1)}}$是$Q$排序中的最优被评价对象, ${{k}^{(2)}}$是$Q$排序中的次优被评价对象, $m$为被评价对象的总个数;

②${{k}^{(1)}}$是$S$或$R$的最优评价对象。

如果条件②不满足, ${{k}^{(1)}}$和${{k}^{(2)}}$均是折衷解; 如果条件①不满足, 方案${{k}^{(1)}}{{k}^{(2)}}\cdot \cdot \cdot {{k}^{(t)}}$是折衷解, 其中${{k}^{(t)}}$满足$Q({{k}^{(t)}})-Q({{k}^{(1)}})\ge 1/(m-1)$。

本研究数据来源于新疆某监狱。选取监狱正在服刑的1 100名监犯的62个维度的监犯基本信息与犯罪数据, 内容包含职业背景、犯罪事实描述、刑期、身高、体重、罪名、犯罪类型、处遇等级、籍贯、前科、家庭成员等。结合监狱背景知识除去无关数据项, 对剩余8个维度的数据进行数据清洗与转化。对亲属关系、罪名个数、从事职业数量等数据采用统计方法转化; 对地区、是否团伙作案、是否已婚、犯罪类型等数据先用正则表达式提取关键词并分类, 再通过二值化转化数据; 对刑期采用先分类再二值化的方法处理。其中, 犯罪类型是针对4类风险倾向划分的:

(1) 心理问题型犯罪: 罪名中包括“强奸|奸淫|儿童|卖淫|歧视|放火|投放”, 这些犯罪大多是因为心理问题;

(2) 暴力型犯罪: 罪名中包括“绑架|故意毁坏|杀人|故意伤害|抢劫|放火|寻衅滋事|破坏|黑社会|爆炸物|枪支”, 这些罪都包含暴力成分;

(3) 教唆他人型犯罪: 罪名中包括“诈骗|分裂|煽动|迷信|犯罪方法|领导|宣扬|传销”, 这些罪基本是组织中的教唆者所犯的;

(4) 缺乏辨识型犯罪: 罪名中包括: “扰乱|窝藏|包庇|参加”, 这些罪一般是被人指使所犯的。

而团伙作案与是否已婚的关键字分别是“伙同|同案”和“夫妻”。最终处理出16项数据项, 分别是代表4个刑期范围的4项刑期范围集标注, 代表不同犯人籍贯的4项地区标注, 代表不同犯罪类型的4项数据, 以及亲属数量、从事职业数量、是否团伙作案、是否已婚4项数据项。将数据集分为待标注训练集和效果评估集, 16项数据项如表2所示。

基于区间模糊VIKOR的监犯特征风险模型旨在通过若干监狱专家对各监犯4类特征风险在区间[0,1]上进行区间模糊打分, 其数值代表该监犯此类风险的程度, 如公式(6)所示。

其中, ${{x}_{ij}}$表示第i个监犯的第j个风险特征的区间模糊风险值。

根据各位专家对某一监犯4项特征风险的区间模糊标注集建立区间数型指标决策矩阵, 进一步通过区间模糊VIKOR算法计算, 对专家标注集进行排序, 以排在第一的专家标注作为此监犯最终的4项特征风险数值。以此方法得到最符合监犯实际特征的4项特征风险数值。

从样本数据中随机选取213个监犯的数据, 用于区间模糊VIKOR监犯特征风险的计算。与监狱方沟通后, 得到4位专家分别标注的原始样本标注集, 某一监犯的原始样本标注如表3所示。

基于区间模糊VIKOR对监犯特征风险进行标注集优化。

(1) 以样本标注为指标决策矩阵, 计算正负理想解, 将4项风险指标视为效益型指标, 该犯风险的正理想解${{f}^{+}}=[0.25,0.40,0.45,0.30]$, 负理想解${{f}^{-}}=$ $[0.15,0.30,0.40,0.20]$。

(2) 根据该犯指标决策矩阵以及计算公式, 得到4位评估专家的打分结果, 由于4种风险类型并无优劣之分, 因此权重都为0.25。经计算, 群体效益区间值下限${{S}^{L}}=[0.5,0.125,0.625,0.125]$, 群体效益区间值上限${{S}^{U}}=[1.75,1.125,2.125,2.0]$, 个体遗憾区间值下限${{R}^{L}}=[0.25,0.125,0.25,0.125]$, 个体遗憾区间值上限${{R}^{U}}=[0.5,0.375,0.75,1.0]$。

(3) 根据4位专家打分情况的群体效益区间值以及个体遗憾区间值, 计算利益比率区间值下限${{Q}^{L}}=[0.17,0.0,0.20,0.0]$, 利益比率区间值上限${{Q}^{U}}=[0.62,0.40,0.86,0.97]$, 由此上下限计算出4个打分方案的利益比率值$Q=[0.40,0.20,0.53,0.48]$, 因此最合适的方案是第二种方案。

(4) 计算该犯最终4项倾向指标, 将第二种方案的区间值转化为单一数值作为最终结果, 采用区间值转化的一般方法, 取其上下限的中值作为最终结果。因此, 该犯最终的计算结果如表4所示。

利用以上方法对每一个标注集中的犯人进行区间模糊VIKOR计算, 得到最终4项特征倾向数值, 其结果作为下一步机器学习算法的训练集与测试集。与传统布尔型人工标注集相比, 本研究优化后的标注集考虑人在评估时的不确定性与模糊性, 使结果更加符合实际。

考虑到单一机器学习算法的局限性与监狱数据的复杂性, 不同机器学习算法对于监狱数据集的预测效果会有差异, 因此综合比较多种机器学习算法, 选择预测效果最好的作为最终模型。将3.3节监犯倾向结果作为监犯特征风险预测模型的训练目标, 而将数据预处理所得到的细分后的16项数据作为训练数据。对这16项数据进一步处理以提高训练精度: 进行特征提取, 计算每种数据项的特征值, 除去特征值过小的数据项, 即“亲属数量”、“是否已婚”、“是否团伙作案”三个维度; 进行归一化处理。为降低过拟合情况, 将数据集拆分为训练集和测试集, 用于交叉验证。

本文研究的训练目标“犯事倾向程度”是连续型变量, 因此选用机器学习中的回归算法作为训练模型, 选取神经网络、随机森林、决策树、支持向量机(SVM)、K近邻(KNN)和XGBoost共6种算法, 分别以4种倾向之一的数值作为训练目标进行模型训练。对不同算法分别进行调参, 得到使各算法精度最高的模型参数。以拟合优度${{R}^{2}}$作为回归模型的评价指标, ${{R}^{2}}$等于回归平方和在总平方和中所占的比率, 即回归方程所能解释的因变量变异性的百分比, 范围在0到100%之间, 数值越大说明模型的拟合程度越高。各算法模型对暴力型倾向的拟合优度如表5所示。由于篇幅限制, 其余三类倾向训练结果不再列出。

其余三类倾向的模型训练方法相同, 但不同算法对于4类倾向的预测结果优劣不同。根据数据集训练结果, 各倾向选取使其拟合优度最大的机器学习模型作为预测模型。暴力型倾向选取决策树作为监犯特征风险预测模型; 心理问题型倾向选取SVM作为预测模型; 教唆他人型倾向选取KNN作为预测模型; 缺乏辨识型倾向选取随机森林作为预测模型。究其原因, 以暴力型倾向为例, 新疆地区监犯暴力特征明显, 专家在标注时已根据其特征做出较为经验的判断, 而决策树算法是根据监犯各指标进行分枝, 特征识别性较明显, 最符合新疆暴力犯特征; SVM算法在样本量较少的情况下相比于其他算法更优, 但在样本量较多时可能不如其他算法。由此可见, 对于不同监狱难以确定一种固定的机器学习算法进行预测, 需要结合监狱的数据特征、可分析样本量等因素, 将多种机器学习算法综合使用才能训练出最适合本监狱的风险评估模型。

将此综合模型(暴力型: 决策树; 心理问题型: SVM; 教唆他人型: KNN; 缺乏辨识型: 随机森林)应用于验证集数据中, 预测出每位犯人的4项倾向值。由于现有监犯风险评估模型的结果都为单一风险值, 为与现有模型作对比, 将4项倾向值取算数平均。部分监犯犯事倾向预测结果与算数平均值结果如表6所示。

(1) 测试集指标选择

本研究的数据中最有效反映犯人在监狱表现的数据项是处遇等级, 罪名重大的犯人入狱时会被判处严管, 当在监狱内犯事后降低其处遇等级以作为惩罚, 最低降到一级严管。同理其他类型的一级一般也是犯事后降级的, 诸如普管一级、危安一级等, 因此以各类一级为犯人在监狱犯事的标志。

(2) 待对比现有模型

从现有监狱风险评估研究中选出准确率较高的 评估模型, 即Logistic回归模型^[9], 回归方程如公式(7)所示。

其中, ${{X}_{1}}$表示第一次犯罪年龄, ${{X}_{2}}$和${{X}_{3}}$代表不同文化程度, ${{X}_{4}}$和${{X}_{5}}$代表不同地区, ${{X}_{6}}$代表团伙人数, ${{X}_{7}}\tilde{\ }{{X}_{10}}$代表不同刑期范围, ${{X}_{11}}\tilde{\ }{{X}_{14}}$代表不同犯罪类型, ${{X}_{15}}$代表表态分数。Logistic回归的结果即为分类置信度, 可以表示监犯风险程度。

(3) 最佳分割点确定

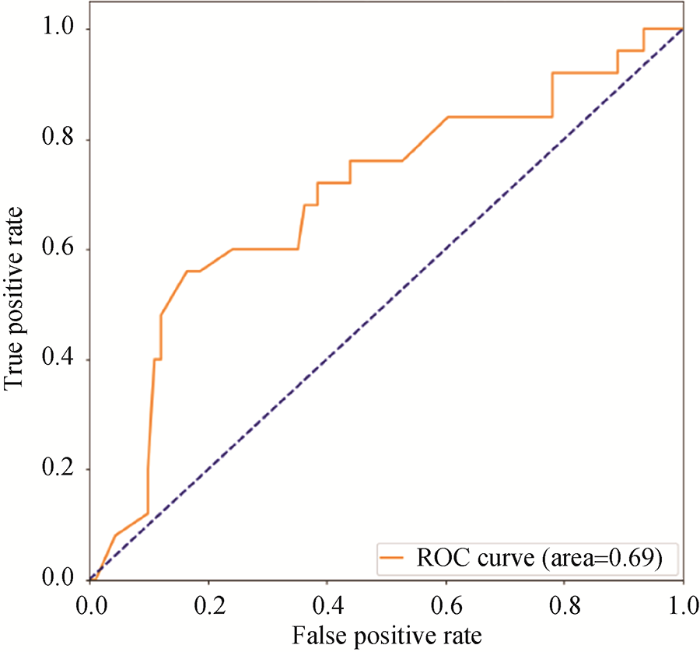
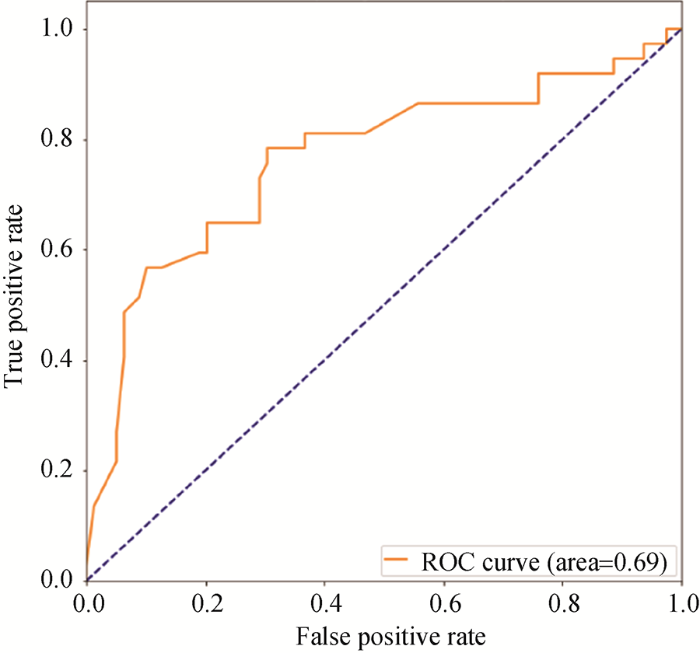
在计算模型准确率之前, 需要找到分类效果最佳的监犯风险数值分割点, 此分割点以下数值表示监犯不会犯事, 分割点以上数值表示会犯事, 根据ROC曲线判断最佳分割点位置。ROC曲线是根据一系列不同的二分类方式(分界值或决定阈), 以真阳性率(灵敏度)为纵坐标, 假阳性率(1-特异度)为横坐标绘制的曲线。曲线上最靠近坐标轴左上角的点即为最佳分割点, 而AUC值为ROC曲线所覆盖的区域面积, AUC越大, 分类器分类效果越好。

将对比模型的Logistic回归方程代入评估效果验证集, 得到每个犯人犯事风险的评估值。根据ROC曲线确立该模型的最佳分割点为0.39, AUC为0.69, 如图2所示。监犯特征风险评估模型所得结果的ROC曲线如图3所示, 其最佳分割点为0.31, AUC为0.79。

(4) 模型对比评估

由于验证集指标是0-1分布, 因此采用分类模型评估方法, 选取混淆矩阵中二级指标的精确率(Precision)、召回率(Recall)和三级指标F1-Score评估模型。经最佳分割点分割后, 对比模型(Logistic回归)的混淆矩阵如表7所示。根据此混淆矩阵可知, 对比模型预测犯事的精确率为70.0%, 召回率为68.8%, F₁为0.69。

本文组合评估模型的混淆矩阵如表8所示。根据此混淆矩阵可知, 本文模型预测犯事的精确率为78.9%, 召回率为79.9%, F₁为0.79。

本文的组合模型在三个指标下都优于现有监犯风险模型, 模型有效性得到验证。

表6中的监犯犯事倾向预测即为本研究最终结果的部分展示, 可以看出, 第1个犯人表现良好, 第2个和第3个犯人有较高的暴力倾向, 第4个犯人有相当高的教唆他人倾向。在模型验证中, 由ROC曲线得到平均倾向值在0.31以上的监犯存在犯事风险, 结合表6结果可知, 第3个监犯存在暴力斗殴风险, 第4个监犯存在教唆他人闹事风险。在监狱管理过程中, 可根据此研究结果对这些存在风险的监犯进行针对性管理, 例如利用调监措施将暴力型监犯分离、教唆犯与缺乏辨识犯分离等, 或是进行针对性教育, 如对教唆犯和缺乏辨识犯进行法制教育等。

本文将单一评估特征分为若干类具体特征, 用改进的区间模糊VIKOR算法得到最合理的区间模糊评价方案, 再将所得标注集与其他历史数据结合, 用多种机器学习算法建模, 得到监犯风险预测模型, 计算监犯4类犯事倾向数值。通过与传统监狱风险评估方法的计算结果对比, 证明了本文基于区间模糊VIKOR的监犯风险评估模型的有效性和适用性。

本文改进传统VIKOR, 减小了指标相关性造成的误差。评估结果能客观反映监犯特征风险, 便于监狱管理人员采取对应管制措施, 一方面为分级管理、分类管理打下基础, 另一方面可以结合宏观的犯人间交互情况, 更好地预防监狱风险事件。

但由于本文的数据量级下机器学习算法原理无明显优劣, 无法对4类特征风险确定某一建模算法更优, 因此应用于其他监狱时需要采用本文方法进行算法比较, 影响了评估建模的效率。由于本文所研究的4类倾向具有交互性, 如教唆型犯人遇到缺乏辨识型犯人时, 其犯事可能性更大, 因此未来可研究不同特征的监犯之间的交互, 进一步帮助监狱管理者改善监狱管理现状。