近年来, 各类数据分析方法和预测模型在临床医学中得到了广泛的应用, 在急救临床实践中, 由于患者伤情往往较为严重, 抢救操作时间紧急, 需要进行快速决策, 而患者的生理、化验指标体系又非常庞大, 为医生快速识别患者关键指标、对患者状态做出正确预测增加了难度^[1]。

当指标数量较少时, 筛选关键指标较为容易, 可采用基于样本状态识别率的包裹式或嵌入式方法计算指标重要性, 再依据实际需要截取满足条件的关键指标。但是, 当患者生理、化验指标数量较多时, 会大大增加上述方法的迭代复杂性, 而且指标数量截取的标准难以统一, 为医生进行全方位、多角度判断增加了难度, 此时, 关键指标的筛选就需要同时考虑保留的指标数量与样本状态识别精度两个方面。本文针对这一问题, 选取一个新的视角, 即将多目标优化中的帕累托最优思想与机器学习进行有机结合, 提出一种实现指标数量与患者状态识别精度同时优化的关键指标筛选方法, 并与既有方法进行比较。

在近期的急救患者关键指标及后续状态预测研究方面, Jones等^[2]建立了急救患者5大指标与治疗时间的线性回归模型, 分析了各项指标与治疗时间之间的关系; Coster等^[3]通过对6个月的患者报告进行统计性分析, 提出了患者发生重伤的急救场景下与7日内存活率相关的关键指标; McCoy等^[4]运用机器学习算法实现了具有较高死亡率的脓毒症患者的风险评分, 为病情的早期干预提供了决策支持, 患者指标体系的构建则通过人工筛选进行; Gupta等^[5]在两套不同的脓毒症诊断指标体系下, 分别运用决策树、逻辑回归、朴素贝叶斯等方法预测病人死亡率, 判别了两套指标体系的优劣; Levin等^[6]针对美国急救领域内患者的治疗标准与风险分级严重依赖主观经验方法的缺陷, 采用随机森林算法, 基于患者重要历史治疗数据对其结局进行预测, 获得了比主观方法更高的精度; Hohl等^[7]采用前瞻性研究方法(Prospective Study)结合收集到的患者各项指标, 建立了两套对急救患者实施药剂师为主导的药物治疗决策规则, 在实际运用中获得了较高的诊断准确率。

由上述研究可见, 对于急救患者的结局预测、风险预警研究, 相对于传统方法, 机器学习已经取得了较好的效果, 但患者关键指标体系的建立依然多依赖于较为单一的决策目标或筛选原则(如仅依赖精度评价指标), 在特征数量和状态识别精度之间的权衡方法研究较少, 尤其是在指标规模庞大时, 这一研究的意义更为突出。

周志华^[8]将机器学习领域的特征选择方法分为三类, 分别是: 过滤式方法; 包裹式方法; 嵌入式方法。其中, 过滤式方法将特征的选取与后续的模型训练分割为两个独立的部分, 例如Relief方法^[9]、基于粗糙集的属性约简^[10]等, 由于未考虑后续学习器的性能, 因此该方法所选取的特征依然有可能存在冗余, 即容易造成后续模型的过拟合; 包裹式方法则直接把最终使用的学习器的性能作为指标选取的评价标准, 因此, 其特征选取的效果优于过滤式方法; 嵌入式特征选择将特征选择过程与机器学习训练过程融为一体, 即在学习器训练的过程中自动进行特征选择, 常见的嵌入式方法有L1正则化^[11]、随机森林^[12]等, 而嵌入式方法的效果受数据集构造方式的影响较大。目前, 对于特征选取的研究, 由于包裹式方法是直接以后续学习器的性能为目标选取指标, 以该目标为原则, 具体特征选取方法的设计还存在较大的研究空间。

基于包裹式方法的思想, 一些学者以学习器性能为依据选择穷举法^[13]进行特征选择, 对属性集合的所有真子集进行迭代遍历, 寻找最好的属性集合, 显然, 该方法在面对特征数量较大的数据集时运算代价非常大; 针对穷举法的弊端, 有人提出递归式特征消除方法^[14], 其主要思想是反复构建训练模型, 每轮训练结束后, 消除若干权值系数对应的特征, 再基于新的特征集进行下一轮训练; 周成等^[14]提出了一种典型的递归式特征消除方法, 首先, 利用后向递归轮流去除指标后, 考察识别率变化, 据此计算每个指标的“影响系数”, 在后向递归得到的影响系数排序基础上, 利用前向递归依次增加指标, 依据各指标对识别率的贡献计算“提升系数”, 作为属性重要性选取关键指标; Huang等^[15]在递归式特征消除法与支持向量机二者结合的基础上引入特征聚类分析, 提升了寻找关键基因特征的效率; 但递归式特征消除方法也有两个缺陷: 迭代过程依旧复杂, 计算量没有显著下降; 从智能算法的角度而言, 该方法在一定程度上缩小了指标组合的搜索空间, 人为干预因素影响较大, 容易出现属性集合的局部最优。

就优化的角度而言, 当数据集特征数量较多时, 特征选择问题是典型的NP-Hard问题, 一些学者将人工智能算法与数据挖掘算法进行有机结合, 将特征选择问题进行编码, 使其转化为可用智能算法求解的优化问题。Alijla等^[16]将改进的智能水滴算法与基于C4.5、支持向量机等基于包裹式特征选取的机器学习算法相结合, 取得了良好的特征选择效果; Sayed等^[17]采用混沌集群算法选取能够实现最高分类精度的特征子集; Zouache等^[18]则将量子行为与集群智能算法结合, 求解基于粗糙集的属性约简问题, 并取得了良好的效果。目前, 基于智能优化算法的特征选取以单目标优化为主, 同时考虑数据子集所包含特征数量与数据子集分类性能的多目标特征选取尚存较大研究空间。

综上所述, 本文的研究工作主要解决两方面的问题:

(1) 针对医学领域急诊危重患者庞大的指标体系, 目前指标选取多依赖于主观经验的不足, 提出一种基于包裹式方法思想的关键指标筛选方法;

(2) 针对包裹式特征选择方法中易产生NP-Hard问题、迭代过程依然复杂的缺点, 兼顾关键指标数量, 将多目标智能优化算法与机器学习算法有机结合进行指标筛选, 提升患者结局状态识别精度。

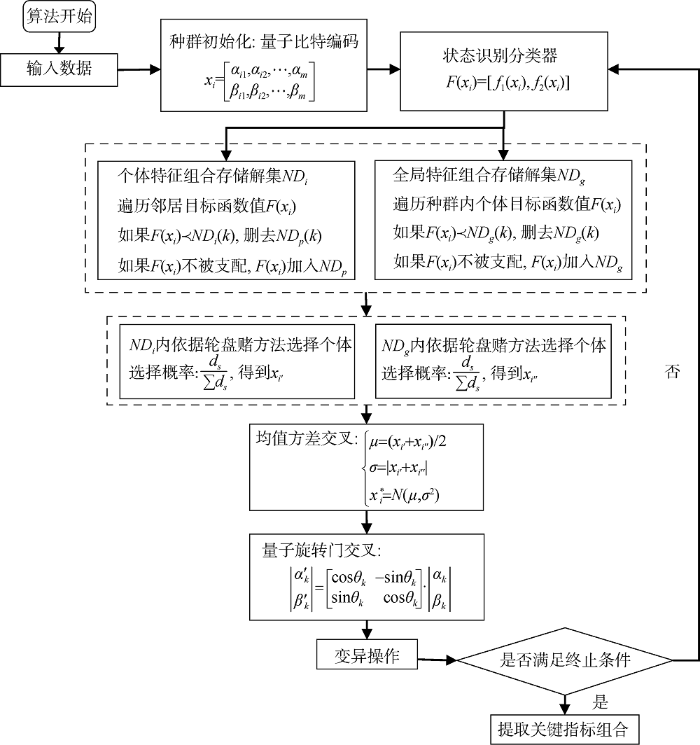
本文将患者关键指标的筛选问题视为综合考虑: 指标约简数量和指标对患者状态识别精度的多目标优化问题。对于该优化问题采用基于量子行为的粒子群算法进行求解, 种群中的每个粒子表示一种指标组合, 指标组合采用量子比特编码, 以该指标组合条件下机器学习的状态识别精度及指标数量作为目标函数, 粒子群内的遗传操作采用量子旋转门、均值方差法及混沌变异相结合的形式进行, 通过粒子群的多次更新, 产生最优的关键指标组合。

量子进化的思想是将量子的状态叠加性、并行性等特性引入进化计算, 通过量子旋转门推动量子的进化, 以解决传统进化算法易早熟的缺点^[19], 量子比特表示如公式(1)所示。

其中, $\alpha $与$\beta $分别以复数的形式表示状态$\left| \text{0} \right\rangle $与状态$\left| \text{1} \right\rangle $的概率幅, 且$\alpha $与$\beta $满足归一化条件${{\left| \alpha \right|}^{\text{2}}}\text{+}{{\left| \beta \right|}^{\text{2}}}\text{=1}$, 这样, 对于具有$m$个初始指标的筛选问题则可以用$m$位量子比特表示, 如公式(2)所示。

可见, 状态$\left| \text{0} \right\rangle $表示非关键指标, 状态$\left| \text{1} \right\rangle $表示关键指标, 长度为$m$的量子比特编码可以表示的经典信息量为${{2}^{m}}$, 可通过较少的迭代步数实现更加广泛的搜索空间, 在指标数量较多的情形下, 可以极大提升筛选性能。将不同的指标量子比特编码视为一个种群, 种群的状态进化可通过量子旋转门$U$实现, 依据薛定谔方程要求, 旋转门应满足$U\cdot {U}'=1$, 如公式(3)所示。

其中, ${{\theta }_{k}}$为调整策略, 由粒子当前适应度与种群中优秀个体比较得到, 调整策略的设计有固定的规则, 此处不再赘述。由此, 可通过量子旋转门调整种群中个体指标组合向优秀粒子的进化, 实现关键指标筛选。

关键指标筛选的原则是在去掉冗余指标的同时保证患者状态识别精度达到要求, 以指标组合情况为自变量, 令${{x}^{R}}$表示指标组合情况的实数编码, 可将该原则用多目标规划的形式表示, 如公式(4)所示。

进一步, 公式(4)可表示为标准形式, 如公式(5)所示。

其中, $G$表示各种基于机器学习的状态识别(分类)算法精度, ${{{f}'}_{1}}$与${{{f}'}_{2}}$分别表示${{f}_{1}}$与${{f}_{2}}$的标准形式(${{{f}'}_{2}}$即表示状态识别误差)。可见, 由机器学习算法自身的特点可知, 上述多目标优化问题的各个子目标之间具有矛盾性。因此, 本文引入帕累托最优解思想进行去除冗余指标与保证患者状态识别精度之间的权衡。

定义1: 关键指标组合支配关系。对于指标组合${{x}_{A}},{{x}_{B}}\in S$, 如果有${{{f}'}_{i}}({{x}_{A}})\le {{{f}'}_{i}}({{x}_{B}})$$(i=1,2,\cdots ,n)$且至少存在一个$j\in \left\{ 1,2,\cdots ,n \right\}$使${{{f}'}_{j}}({{x}_{A}})<{{{f}'}_{j}}({{x}_{B}})$, 则称关键指标组合${{x}_{A}}$支配关键指标组合${{x}_{B}}$, 记作${{x}_{A}}\prec {{x}_{B}}$。

定义2: 非支配关键指标组合。如果关键指标组合${{x}_{C}}\in S$并且${{x}_{C}}$不被其他任何关键指标支配, 则称${{x}_{C}}$为非支配关键指标组合。

定义3: 关键指标筛选的帕累托前沿。由所有非支配关键指标组合计算得出的目标函数值集合在解空间中的表示称为关键指标筛选的帕累托前沿(表示为$PF$), 如公式(6)所示。

本文将改进的多目标粒子群算法与量子行为进行结合, 作为指标筛选优化算法, 其中, 选取粒子群算法作为基础算法的原因是: 相对于一般的智能算法, 粒子群算法具有更快的收敛速度, 有助于提升指标选取效率; 而量子行为的引入, 又可以在算法的探索能力(Exploration)与开发能力(Exploitation)之间取得较好的均衡^[18], 避免指标选取陷入局部最优。

步骤1: 粒子种群初始化。设置粒子群的规模$N$、种群内个体非支配解集$N{{D}_{i}}$及全局非支配解集$N{{D}_{g}}$的存储容量、迭代次数。利用公式(2)对种群内的粒子$i$进行量子比特编码, 即${{x}_{i}}=\left[ \begin{align} & {{\alpha }_{i1}},{{\alpha }_{i2}},\cdots ,{{\alpha }_{m}} \\ & {{\beta }_{i1}},{{\beta }_{i2}},\cdots ,{{\beta }_{im}} \\ \end{align} \right]$, 相应的解表示为$F({{x}_{i}})=[{{f}_{1}}({{x}_{i}}),{{f}_{2}}({{x}_{i}})]$。

步骤2: 计算每一个粒子所代表的长度为$m$(指标数量)的量子比特编码, 以每个粒子所代表的指标组合作为机器学习算法的输入。本文选取三种典型的、并被广泛采用的机器学习算法对由指标组合构成的数据集进行训练, 分别是: 深层感知机(MLP)^[20]、随机森林(RF)^[21]和K近邻(KNN)^[22]。MLP、RF及KNN均是分类精度较高的算法。KNN对异常值不敏感, RF善于处理分类不均衡的数据集, 且被广泛用于状态识别, MLP由于其学习性能常被作为集成学习的基分类器, 因此, 本文选取上述三种算法。

计算利用该指标组合训练得到的患者状态识别率(随机五折交叉验证法, 训练50次, 目标函数值取状态识别率的均值), 作为对应的目标函数值$F({{x}_{i}})= [{{f}_{1}}({{x}_{i}}),{{f}_{2}}({{x}_{i}})]$, 将$F({{x}_{i}})$分别添加进入$N{{D}_{i}}$与$N{{D}_{g}}$, 具体添加规则如下:

对于任意非支配条件属性解集$ND (ND=N{{D}_{i}},N{{D}_{g}})$内的解$ND(k)$

IF $F({{x}_{i}})\prec ND(k)$

在$ND$内删去$ND(k)$;

ELSE IF $F({{x}_{i}})$不被任何$ND$内的解支配

将$F({{x}_{i}})$加入$ND$;

END

步骤3: 计算$ND$$(ND=N{{D}_{i}},N{{D}_{g}})$内的拥挤距离, 拥挤距离是评价最优解在帕累托前沿上分布均匀性的依据, 本文采用欧氏距离测算:

假设解集$ND$内存储了$K$组解, 首先依据目标函数值${{f}_{r}}({{x}_{s}})$对$ND$中的粒子进行降序排列, 得到具有新索引的目标函数值${{{f}'}_{r}}({{x}_{s}})$, 其中$r$表示目标函数索引, 在本文的关键指标筛选问题中, $r=1,2$, $s\in [1,K]$, 则$ND$中目标函数$r$第$s$组解的拥挤距离如公式(7)所示。

则第$s$组解的总体拥挤距离为${{d}_{s}}=\sum\limits_{r=1}^{2}{{{d}_{s,r}}}$。

步骤4: 依据拥挤距离, 在$ND$$(ND=N{{D}_{i}},N{{D}_{g}})$内选择“个体历史最优量子比特编码”及“全局最优量子比特编码”, 选择方式采用进化计算中常见的“轮盘赌”方式进行: 记$\sum\limits_{s=1}^{K}{{{d}_{s}}}$为$ND$中的拥挤距离之和, 则依据轮盘赌规则, 第$s$组解所对应的粒子被选中的概率为$\frac{{{d}_{s}}}{\sum{{{d}_{s}}}}$, 在$N{{D}_{i}}$中选出的个体记作${i}'$, 在$N{{D}_{g}}$中选出的个体记作${{i}'}'$。

步骤5: 基于量子旋转门与均值方差法的粒子状态更新。将粒子$i$当前的量子比特编码${{x}_{i}}$, 历史最优量子比特编码${{x}_{{{i}'}}}$与全局最优量子比特编码${{x}_{{{{i}'}'}}}$分别转换为实数编码, 分别以$x_{i}^{R}$, $x_{{{i}'}}^{R}$与$x_{{{{i}'}'}}^{R}$表示($x_{i}^{R}=\{x_{i1}^{R},\cdots ,x_{ik}^{R},\cdots x_{im}^{R}\}$), 令$\mu _{i}^{R}=(x_{{{i}'}}^{R}+x_{{{{i}'}'}}^{R})/2$(其量子比特编码则用${{\mu }_{i}}$表示), 令$\sigma =\left| x_{{{i}'}}^{R}-x_{{{{i}'}'}}^{R} \right|$, 则依据“均值方差”交叉算子得到^[23]公式(8)。

令${{p}_{s}}$表示粒子更新方式选择概率。

IF $rand<{{p}_{s}}$

比较$F(x_{i}^{R})$与$F(x_{i}^{R*})$, 将单目标量子优化算法中的旋转角调整策略进行概念迁移, 设计多目标条件下的旋转角调整策略:${{\theta }_{ik}}=\Delta {{\theta }_{ik}}\cdot s({{\alpha }_{ik}},{{\beta }_{ik}})$, 其中, $\Delta {{\theta }_{ik}}$表示旋转角度, $s({{\alpha }_{ik}},{{\beta }_{ik}})$表示旋转方向; 或依据量子比特编码的归一化条件将$x_{i}^{R}$与$x_{i}^{R*}$转化为角度后进行旋转门操作。

确定旋转角调整策略(表1)后, 依据公式(3)更新粒子飞行位置。

ELSE

设置${{p}_{c}}$为交叉概率, 令$x_{i}^{R*}$中的实数编码变量$x_{ik}^{R*}$($k=1,\cdots ,m$)以概率${{p}_{c}}$变换为$x_{{i}'k}^{R}$, 后以概率${{p}_{c}}$变换为$x_{{{i}'}'k}^{R}$

END

步骤6: 混沌变异。设置${{p}_{m}}$为变异概率, 在粒子群中以概率${{p}_{m}}$选择粒子, 对于选中的粒子$i$, 采用Tent映射对其变量$x_{ik}^{R}$迭代$t$次, 如公式(9)所示。

步骤7: 当指标筛选满足条件(帕累托前沿不再变化)时, 结束, 否则返回步骤2。可见, 上述算法的时间复杂度为$O({{n}^{3}})$。

基于上述指标筛选算法的执行机理, 本文将该算法命名为量子行为多目标粒子群优化算法(Quantum Bare-Bones Multi-Objective Particle Swarm Optimization Algorithm, QBBMOPSO)。算法流程如 图1所示。

(1) 关键指标提取

由上述算法得到的关键指标组合帕累托前沿为医生提供了一套指标数量与患者状态识别精度之间的权衡方案。进一步, 医生可依据急救临床实践不同抢救方案的过往经验给出患者状态识别精度的阈值要求, 并依据该阈值筛选满足条件的非支配关键指标组合。

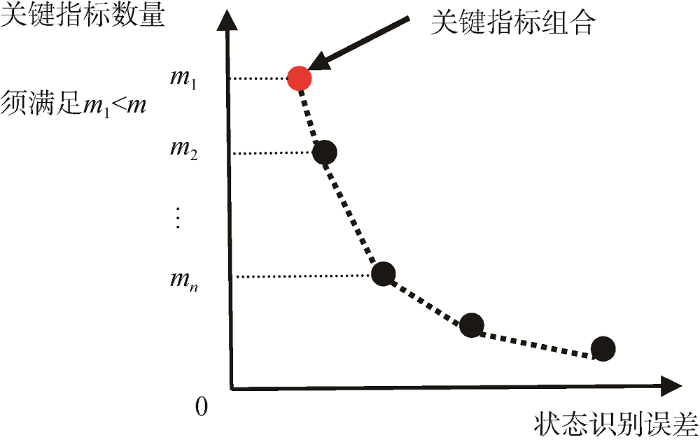
如图2所示, 每一种指标数量条件下能够获取的最大状态识别精度(或每种精度下的最小指标数量),关键指标的选取则可以以患者状态识别精度为标准截取满足条件的非支配关键指标组合(精度阈值左侧的非支配关键指标组合)。

需要注意的是, 当关键指标组合帕累托前沿中的最大关键指标数量${{m}_{1}}<m$时, 说明既有指标体系数据中存在指标冗余, 通过算法迭代, 本文选取患者状态识别精度最高(状态识别误差最低)且最大关键指标数量值(${{m}_{1}}$值)最小的指标组合所对应的帕累托前沿, 该指标组合即作为关键指标。

(2) 关键指标重要性计算

令${{C}^{*}}$表示所有满足状态识别精度阈值要求的关键指标, 令$C$表示全部指标集合, 结合基于前向递归思想的“提升系数”策略^[14], 将关键指标重要性定义如公式(10)所示。其中, $G$表示基于机器学习的状态识别(分类)算法精度。

实施步骤如下:

①基于指标集$C-{{C}^{*}}$建立分类器, 计算识别率为$G(C-{{C}^{*}})$。

②For指标集合${{C}^{*}}$

计算$G(C-{{C}^{*}}+C_{i}^{*})$100次

End

③依据公式(8)计算${{w}_{i}}$, 得到关键指标重要性。

虽然上述步骤借鉴了前向递归思想中的“提升系数”策略, 但与递归思想不同的是, 上述步骤仅需对筛选出的关键指标进行单向迭代, 无需嵌套循环, 显著减小了迭代次数。

本文数据来源是中国人民解放军总医院提供的365个进行插管与按压抢救的病例及其65项进行抢救时数据质量较好的生命体征与化验指标数据(其中, 生命体征指标16项, 化验指标49项), 如表2所示。此外, 患者的结局状态(治愈、死亡)作为分类标签(其中97个为死亡病例), 对于原始数据中的空缺值, 均采用逐列进行均值填充的方法。其中, 指标编号1-49为化验指标, 指标编号50-65为生命体征指标。

如后文无特别说明, 算法参数按表3取值。

为了全方位提升基于机器学习分类器的指标筛选算法性能, 对本文方法分别进行两个维度的比较, 第一个维度从多目标优化算法性能的角度出发, 将本文的指标筛选优化算法与多目标粒子群优化算法(Multi- Objective Particle Swarm Optimization Algorithm, MOPSO)^[23]进行比较, 并选取用于指标筛选的分类器; 第二个维度则从不同分类器的性能角度出发, 在本文提出方法的基础上选取用于患者状态识别的分类器。

(1) 指标筛选优化算法性能对比

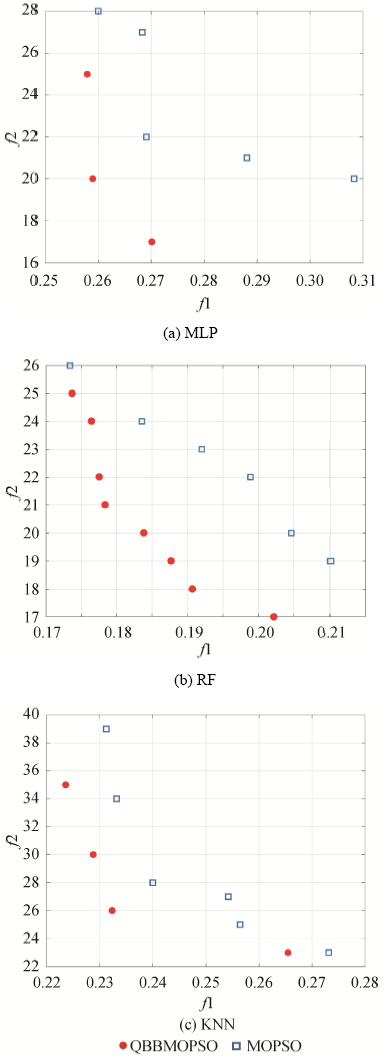
图3给出了具有代表性的不同指标筛选优化算法得到的帕累托前沿, 可见, 相对于其他两种算法, QBBMOPSO算法可以分别在不同分类器条件下更好地实现利用较少数量的指标获取较高的状态识别精度, 相同算法迭代步数下效果最好。此外, 就三种分类器的预测准确率而言, RF分类器可以获得更高的识别准确率(识别误差小), 因此, 选取RF作为用于指标筛选的基分类器。

对于一些典型的连续多目标优化问题, 帕累托前沿的理论值往往比较容易得到, 而对于由实际数据分析筛选的离散多目标优化问题, 帕累托前沿的理论值往往无法获得。近年来, “支配率”被很多学者用来衡量无法获取帕累托前沿理论值的多目标优化问题的计算性能, 本文则沿用这一指标。支配率如公式(11)所示。

其中, $S{{C}_{AB}}$表示算法$\mathrm{B}$得到的指标组合被算法$\mathrm{A}$得到的指标组合支配的百分比, 显然, $S{{C}_{AB}}$值越大, 表明算法$\mathrm{A}$效果越好, 令$S{{C}_{A}}$表示算法$\mathrm{A}$对其他算法筛选出指标组合的支配率。

由表4可见, 以本文提供的数据集为基础, QBBMOPSO算法明显得到了表现更加优异的表现, 该算法得到的帕累托最优解对其他算法得到的帕累托最优解具有更高的支配率, 说明本文提出的指标筛选方法在优化性能方面的有效性。

(2) 关键指标筛选结果

采用3.3节与3.4节的方法, 多次重复实验, 选取患者状态识别精度最高且最大关键指标数量(m₁值)最小的帕累托最优解所对应的指标组合作为关键指标组合, 筛选出的关键指标及其重要性如表5所示。

各指标含义如下:

①γ-谷氨酰基转移酶: 对各种肝胆疾病均有一定的临床应用价值, 可用于鉴别肝脏系统疾病。

②国际标准化比值: 患者凝血酶原时间与正常对照凝血酶原时间之比的ISI次方(ISI: 国际敏感度指数)。

③红细胞比积: 每升血液中红细胞所占的容积。

④肌钙蛋白T: 肌肉组织收缩的调节蛋白, 在肌肉收缩和舒张过程中起着重要的调节作用。

⑤肌酐: 肌肉在人体内代谢的产物。

⑥淋巴细胞: 白细胞的一种, 是体积最小的白细胞, 由淋巴器官产生。

⑦钠: 人体内钠含量。

⑧平均红细胞体积: 人体单个红细胞的平均体积。

⑨平均红细胞血红蛋白量: 每升血液中血红蛋白含量/每升血液中红细胞个数。

⑩平均血小板体积测定: 采用自动化血细胞分析仪后得到的一项临床检测指标, 属于血常规检查。

⑪血浆凝血酶原时间测定: 人为加入特殊物质激活外源性凝血途径, 使血液凝固, 监测口服抗凝药用量的首选指标。

⑫血清尿酸: 嘌呤分解代谢的最终产物, 是诊断肾重度受损的敏感指标。

⑬血小板计数: 单位体积血液中所含的血小板数目。某些疾病原因可导致血小板数量的减少或增多, 血小板计数有助于临床上止血和血栓性疾病的诊断和鉴别诊断。

⑭直接胆红素: 由间接胆红素进入肝后受肝内葡萄糖醛酸基转移酶的作用与葡萄糖醛酸结合生成, 常用于黄疸的诊断。

⑮BEecf: 组织间液的剩余碱。

⑯HCO3std: 标准碳酸氢根, 反映机体酸碱调节情况。

⑰pO2: 氧分压, 物理溶解于血液中的氧所产生的张力。

⑱心率: 正常人安静状态下每分钟心跳的次数。

经与实际医生临床经验及指南对比, 本文方法筛选结果中有10项指标具有较为明显的临床意义, 如表6所示。

(3) 患者状态识别分类器性能对比

就机器学习算法自身而言, 仅依靠准确率并不能完全能体现分类器的性能, 尤其是在类别数据分布不均衡的情况下, 分类器完全预测为正类或负类都会产生较高的准确率, 预测的实际价值大大降低。因此, 本文在选取分类器方面, 参考混淆矩阵, 采用综合考虑精确率(Precision)与召回率(Recall)的F-Measure方法评价患者状态识别分类器的性能, F值越大, 表示分类器性能越好, F值计算方法如公式(12)所示。

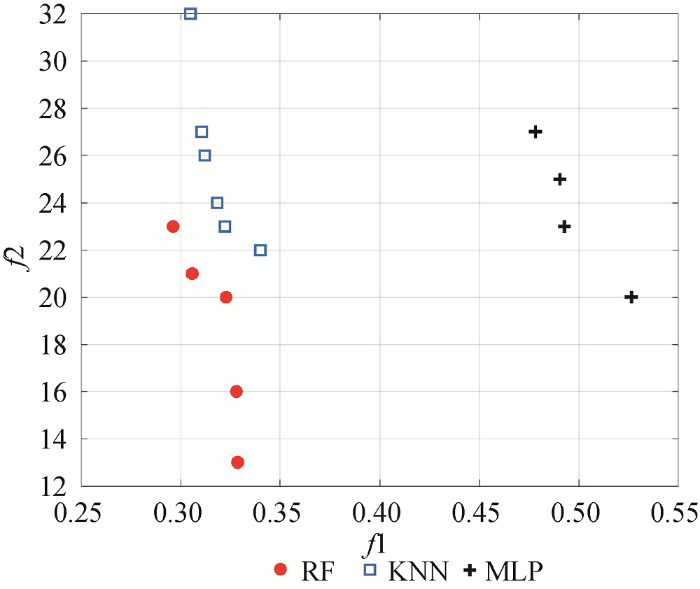
进一步, 将公式(12)带入公式(4)中的f₂, 考察基于不同分类器的帕累托前沿, 结果如图4所示。

由图4可知, RF分类器明显具有质量更好的帕累托前沿; 进一步, 计算不同分类器的平均支配率可得$S{{C}_{RF}}>S{{C}_{KNN}}>S{{C}_{MLP}}$, 可见, 嵌入RF分类器的QBBMOPSO算法具有更好的状态识别性能, 因此, 将RF分类器作为本文的患者状态识别基分类器。

为进一步说明本文所提出方法的有效性, 选取两种常见的并被广泛采用的指标筛选方法进行对比, 分别是基于Gini系数的指标筛选方法以及基于递归式特征消除的指标筛选方法, 考察不同方法所获取的特征对病人最终状态的识别精度、F值。选取的原因在于: 基于Gini系数的指标筛选方法被广泛运用于高维度数据特征选择, 本文也具有较大的指标维度; 此外, 本文提出的筛选方法与递归式特征消除方法均以状态识别精度作为指标贡献度的依据。

Gini系数是随机森林或决策树算法作为切分节点的标准, Gini系数越小, 表明分类效果越好。当数据集中数据混合的程度越高, Gini系数也就越高, 而随机森林算法则是通过计算特征的不纯度以体现指标的重要性, 因此, Gini系数被广泛运用于高维度数据特征选择, 但该方法的效果与数据集自身特点有关。Gini系数定义如公式(13)所示。

其中, $c$表示分类节点, ${{p}_{i}}$表示属于类别i的概率, $K$表示样本类别数, 依据随机森林算法中对指标重要性的计算方法, 计算所有指标的重要性, 按照重要性由高到低排序, 截取与表5相同数量的指标, 如表7所示, 可见, 基于Gini系数选取的重要指标与表5具有差异。就关键指标的临床意义而言, “呼吸”、“舒张压”、“收缩压”是表5与表6未涉及的关键指标。其中, “呼吸”与“pO2(氧分压)”具有等同的临床意义, 可相互替代, 均表征病人与外界的气体交换情况; “舒张压”与“收缩压”反映了病人的血压情况, 当病人发生生命危险时, 血压往往会成为变化明显的指标。总体而言, 表7覆盖表6的临床关键指标较少。

文献[14]同样以样本状态识别率为依据, 针对传统方法的不足, 提出了基于“影响系数”与“提升系数”的递归式特征消除法用来衡量指标重要性, 将文献[14]提出的基于影响系数的提升系数方法引入本文数据集进行计算, 为保证对比在同等条件下进行, 对每个指标影响系数与提升系数的计算采用与本文算法中每个粒子代表的指标组合相同的训练次数(3.4节步骤②), 按照提升系数由高到低排序, 截取提升系数大于0的指标共35个, 如表8所示。

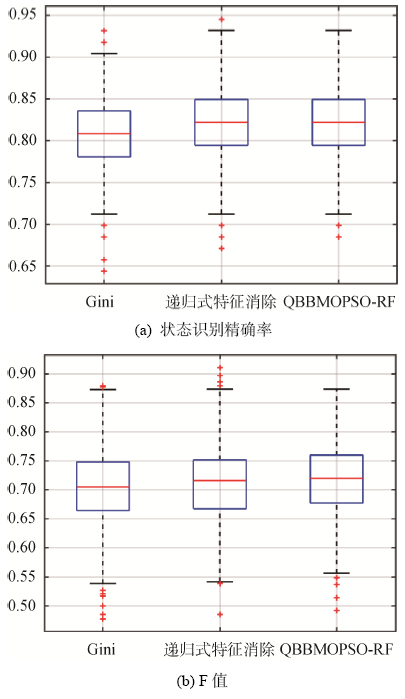
将上述三种方法计算得出的三套关键指标体系作为RF分类器的输入进行训练和预测, 独立实验1 000次, 结果对比如图5和表9所示。

由表9可知, 本文提出的方法可以通过筛选更少数量的关键指标得到更高的患者结局状态识别率与F值, 有效降低了数据维度, 说明了本文方法的有效性。此外, 递归式特征消除法得到的患者状态识别率高于基于Gini系数的方法, 与文献[14]中的方法对比结果一致。

本文基于临床急救数据, 将基于量子行为的多目标粒子群算法与机器学习分类器进行有机结合, 筛选关键指标并计算患者状态识别率, 为医生快速识别患者关键指标、对患者状态做出正确判断提供决策支持。相对于既有的特征选取方法, 本文所提出方法的意义在于通过帕累托最优思想及智能优化算法的引入, 实现了利用更少数量的关键指标获取更高的患者结局状态识别率, 也可以帮助医生获取每一种指标数量条件下的最高患者状态预测精度, 实现了指标数量与患者状态预测精度的同时优化, 为医生提供了一种指标数量截取与权衡的新方法。

本文的局限在于, 多目标优化算法实现指标筛选后, 对于所筛选出的指标权重的计算, 依然要借助部分递归方法。此外, 本文选取的是算法迭代结果中患者状态识别精度最高(状态识别误差最低)且最大关键指标数量值(m₁值)最小的指标组合, 对于在算法运行过程中同样获得了较高患者状态识别精度的其他指标组合, 其医学意义可以进一步做多维度深度研究。并且在实际运用中, 筛选算法也要与医生的治疗经验相结合; 未来的研究中, 当处理的数据规模增大时, 关键指标组合所对应状态识别结果的稳定性也将作为优化目标之一。